터니 암호 해독 방법

책의 6장에 123~125페이지에 나오는, 터니 암호문 해독 방법을 그림으로 조금 더 자세히 설명하면 다음과 같습니다.

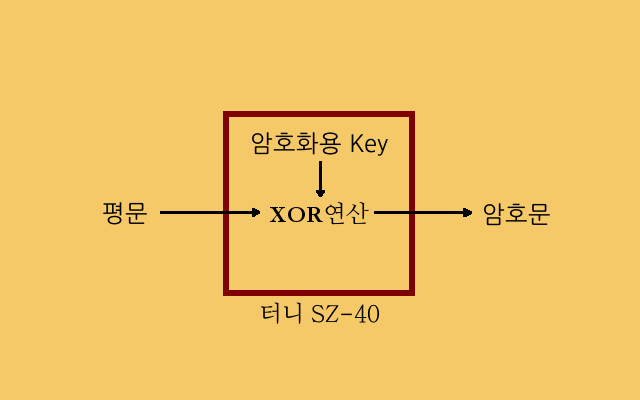
먼저 터니에서 평문을 암호문으로 바꾸는 방법을 개념적으로 단순화해보면 다음의 그림과 같습니다. 터니는 자체적으로 생성하는 key를 평문에 XOR라는 덧셈방식으로 더해서 암호문을 만듭니다.

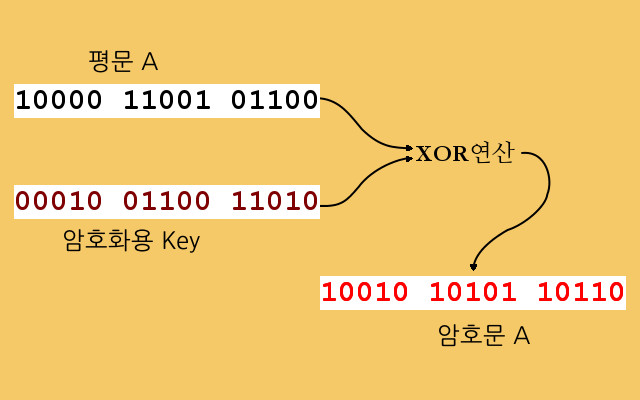
이제 어떤 평문(편의상 ‘평문 A’라고 부르겠습니다)을 암호화하는 예를 보겠습니다. 이 평문은 3개의 문자로 되어 있고, 각 문자는 5비트의 2진수로 표현됩니다. 여기에 터니가 자체적으로 만든 key가 더해지면 암호문이 만들어 집니다. 만들어진 암호문은 편의상 ‘암호문 A’라고 부르겠습니다.

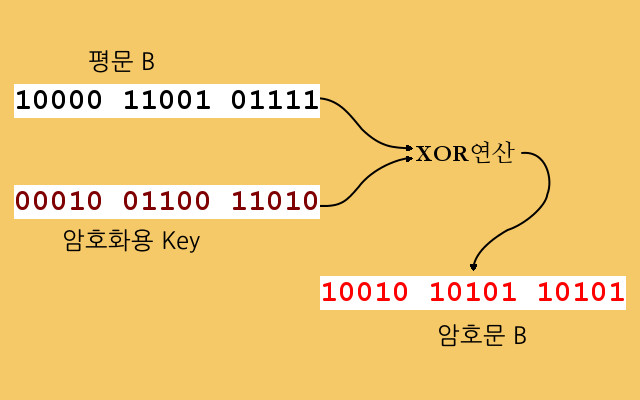
책에서 언급된 바와 같이, 터니의 암호문을 해독하기 위해서는 ‘깊이’가 필요합니다. ‘깊이’는 같은 key를 사용하여 암호화된 두 개의 암호문 쌍을 가리킵니다. 예를 위해서, 또 다른 평문이 같은 key를 써서 암호화 되었다고 가정합시다. 다음의 그림은 또 다른 평문(‘평문 B’)가 앞에서와 같은 key로 암호화되는 것을 보여줍니다. 만들어진 암호문은 편의상 ‘암호문 B’라고 부르겠습니다.

앞에서 만들어진 ‘암호문 A’와 ‘암호문 B’는 같은 key에 의해서 암호화된 것이므로 ‘깊이’에 해당합니다. 이제 암호해독가는 ‘깊이’에 포함된 이 두 개의 암호문을 XOR연산을 써서 서로 더합니다. 그렇게 하면, 양쪽 암호문에 녹아들어가 있던 key값들은 모두 사라지는 효과가 발생하며, 남는 것은 ‘평문 A’와 ‘평문 B’가 XOR연산으로 더해진 것과 같아집니다. 책에서는 이것을 ‘케이크 속에 버터와 설탕이 뒤섞여 있는 것’이라고 표현했습니다. ‘깊이’에 포함된 암호문 두 개가 거의 같고 조금만 차이가 있는 것이라면, 이 결과값은 2진수로 보았을 때, 대부분의 숫자가 0이 될 가능성이 높습니다. 왜냐하면 XOR연산에서는 같은 2진수끼리 더하면 0이 나오기 때문입니다.

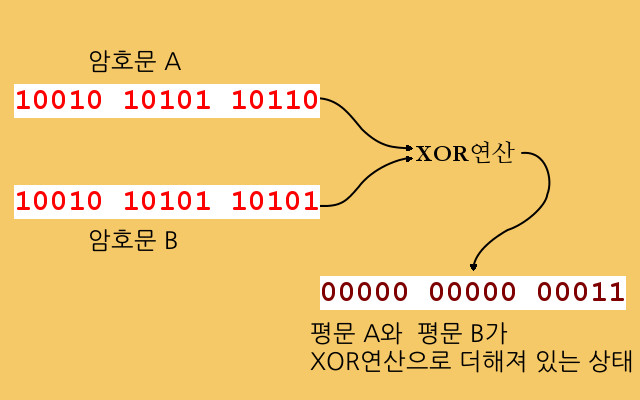
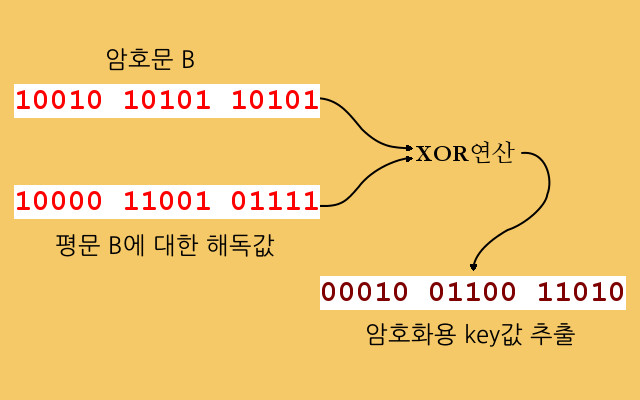
이제 암호해독가는 뭔가 실마리가 될 만한 단어를 하나 생각해 내야 합니다. 이 단어는 순전히 직감에 의한 것일 수도 있고 과거의 해독에서 얻어진 통계적인 추정일 수도 있습니다. 지금의 예에서는 암호해독가가 용케 제대로 유추해 내었다고 가정한 것입니다. (실제 상황에서는 시행착오가 있을 가능성이 높습니다.) 암호해독가는 유추해낸 문자 혹은 단어를 바로 앞에서 계산되어진 결과에 XOR연산을 써서 더하게 됩니다. 그러면, 두 개의 평문 중 나머지 하나가 튀어 나오게 됩니다.

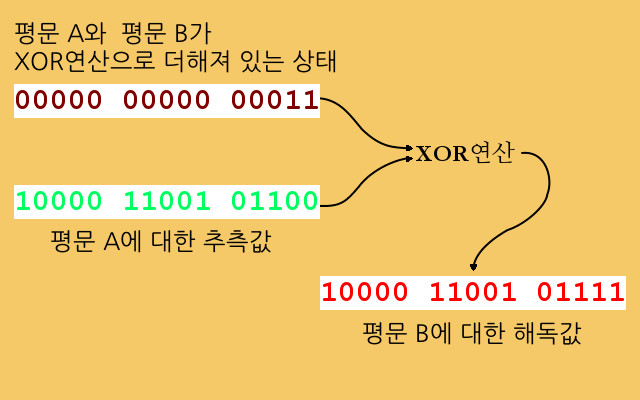
암호해독가가 유추해낸 것이 제대로 맞다는 것이 판명되면, 구한 평문을 원래의 암호문에 XOR연산으로 더해서 key값을 확인할 수 있습니다.