튜링상 관련 업적

계산 복잡도 이론의 기초와 함께 이를 이용한 암호학, 그리고 프로그램 검증 분야에 기여함.

1995년 튜링상 선정 이유

계산 복잡도 (Speedup 정리)

블럼은 래빈의 논문에서 영감을 얻어서, 어떤 함수가 주어졌을 때 “물리적 기계에 영향을 받지 않고 그 함수의 계산 복잡도를 따지는 방법”을 찾고자 했다. <계산가능한 함수의 복잡도에 관한 기계 독립적 이론​2​>에서 그는 두 가지 중요한 이론을 제시했다.

첫 번째는 “물리적 기계에 영향을 받지 않는 계산 복잡도 공식”이 가져야 할 조건이다. 블럼의 공리Blum’s axioms라고 부르는 그 조건은 다음과 같다.

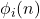  1. 함수 \phi_i(n)이 계산 가능​#​하다면, 그 함수의 계산 복잡도 공식 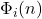\Phi_i(n)도 계산 가능해야 한다.
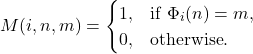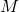  2. M(i, n, m) = \begin{cases} 1, & \text{if} \ \Phi_i(n) = m, \\ 0, & \text{otherwise}.\end{cases} 에서 함수 M도 계산 가능해야 한다.

두 번째는 “최적optimal 알고리듬”에 관한 이론이다. 그는 주어진 함수에 대해서 과연 그 함수를 계산하는 최적의 방법을 찾아낼 수 있을지 궁금했다. 그는 Speedup 정리theorem를 제시했는데 어떤 함수들은 최적, 즉 계산 복잡도가 가장 낮은 방법을 찾을 수 없다고 주장했다. 예를 들어, 정렬이라는 문제(함수)에 대해서 우리가 매우 빠른 방법(알고리듬)을 찾았다고 해도 그것이 정말로 가장 최적의 방법인지는 알 수 없다는 것이다.

중간값 계산 알고리듬

블럼과 거의 동일한 시기에 유리스 하트마니스와 리처드 스턴즈도 계산복잡도에 대한 논문을 발표하였고, 이는 큰 반향을 일으켰다. 어떤 물리적인 기계를 사용할지와 상관없이 알고리듬의 성능을 비교할 수 있는 길이 열리면서 더 좋은 알고리듬을 주장하는 논문이 가능해졌다. 블럼 자신도 그런 변화에 동참했다. 그는 1971년에 <선형 시간 내에 중간값 계산하기​3​>라는 논문을 통해서, 중간값 계산에 관한 획기적인 알고리듬을 발표했다.

중간값이란 여러 개의 수를 크기 순서로 정렬했을 때 가운데에 위치하는 수의 값을 말한다. 예를 들어, 1, 2, 10, 45, 100 과 같이 5개의 수가 있으며, 중간값은 10이다. 중간값은 최대값이나 최소값과 다르게 계산량이 많다. 최대값이나 최소값은 주어진 수들을 한 번만 훑으면 알아낼 수 있다. 숫자의 개수가 10개이면 9번의 비교만 필요하고, 숫자의 개수가 1000개이면 999번의 비교만 필요하다. 따라서 계산량은 숫자의 개수에 비례한다. 이것은 “입력의 개수에 선형 비례한다”라고 표현한다.

이에 비해 중간값은 한 번만 훑어서는 알 수 없다. 여러 번 반복해서 훑어야 한다. 따라서 계산량은 입력의 개수에 선형 비례하지 않고 지수 비례한다.

블럼은 독특한 알고리듬을 개발하여, 중간값을 구하는 계산량이 입력의 개수에 선형 비례하게끔 만들었다. 블럼의 알고리듬도 반복적으로 여러 번 입력 숫자들을 훑는다. 하지만 그때마다 후보에서 제외되는 숫자들의 개수가 많기 때문에 전체적인 수행 성능은 입력의 개수에 선형 비례한다. 이 논문은 스탠퍼드 대학교의 로버트 플로이드​**​, 본 프랫, 로널드 리베스트​††​, 로버트 타잔​‡‡​과의 공동 작업으로 탄생했다. 이들이 제안한 새로운 알고리듬은 다음과 같은 최대 한도upper bound를 보장한다.

103n/18 \approx 5.73n

여기서 n은 입력의 개수이다. 기존의 단순한 알고리듬은 n^2의 계산 복잡도를 가지는데, 만약 n의 값이 작다면 블럼의 방법이 더 계산량이 많을 수도 있지만 n의 값이 커지기 시작하면 훨씬 빠른 결과를 보여준다.

동전 던지기

동전 던지기는 두 사람(A, B)이 뭔가를 정할 때 많이 사용하는 방법이다. 보통은 두 단계로 진행된다.

  • 단계 1) 두 명 중 한 명, 예를 들어 A는 동전의 어느 면으로 갈지를 확인한다.
  • 단계 2) B는 동전을 던져 바닥에 떨어뜨리고 보이는 면을 확인한다.

일반적인 동전 던지기는 두 사람이 함께 있는 상태에서 진행하므로, 결과에 대해 이의를 제기하지 않는다. 사기cheating가 끼어들기 어렵기 때문이다. (물론 마술사가 개입한다면 얘기가 좀 달라…)

하지만 멀리 떨어져 있는 두 사람이 동전 던지기를 하려면 어떻게 해야 할까? 상대방을 속일 수 없어야 할 뿐만 아니라, 속일 수 없다는 사실을 두 사람이 모두 인정하는 방법이 있어야 할 것이다. 블럼은 그 방법을 고안해 냈다. <전화로 동전 던지기 하기: 불가능한 문제를 해결하기 위한 프로토콜​4​>이라는 논문에서 그는 다음과 같은 예를 들면서 그 해결책을 제시했다.

앨리스와 밥은 전화 상으로 동전 던지기를 하고 싶다. (그들은 막 이혼한 사이인데, 다른 도시에 살고 있고, 자동차를 가져갈 사람을 정하려고 한다.) 밥은 자신이 ‘앞면’에 걸겠다고 말했다가 (전화선 반대편에 있는) 앨리스가 “자, 갑니다… 지금 동전을 던졌어요… 뒷면이 나왔네요!”라고 할까 봐 걱정된다.​4​

블럼은 일방향함수one-way function를 사용했다. 일방향함수는 역방향으로는 값을 알아내기 어려운 함수를 말한다. 함수function란 무엇인가? 함수란, 입력값이 주어지면 출력값을 대응해 주는 규칙이다. f(x) = 2n + 1이라는 함수가 하는 일은 입력값이 1일 때는 출력값 3을 대응해주고, 입력값이 4일 때는 출력값 9를 대응해 주는 것이다. 그렇다면 역방향이란, 출력값이 주어지면 입력값을 알아내는 것이다. 그런데 어떤 함수는 순방향의 공식을 알고 있어도 역방향으로 값을 찾아내기 어렵다. 대표적인 것은 소인수분해factorization이다. 예를 들어 f(i, j) = i \times j (단 i, j는 소수)라는 함수가 있다고 하자. 그러면 f(6521, 3557) = 23195197이다. 그런데 23195197을 주고 i, j에 해당하는 값을 구해보라고 하면 상당히 어렵다.

이런 일방향함수를 사용하여 동전 던지기를 구현하면 다음과 같다.

  • 단계 1) 동전을 던지는 사람인 A는 ‘앞면’과 ‘뒷면’ 중 하나를 선택한 후 그것을 일방향함수에 입력한다. 함수의 출력값을 B에게 전송한다.
  • 단계 2) B는 전송받은 출력값을 잘 보관한 후, ‘앞면’으로 갈지 ‘뒷면’으로 갈지 결정한다. 그리고, 결정된 사항을 A에게 전송한다.
  • 단계 3) A는 B의 결정을 전달받으면 자신이 선택했던 값과 일방향함수를 B에게 전송한다.
  • 단계 4) B는 전송받은 값을 일방향함수에 적용해서 그 결과가 단계 2에서 전송받은 값과 일치하는지 확인한다. 일치한다면 A가 처음에 선택한 값을 인정한다.

위의 예에서는 일방향함수를 미리 B에게 공개하지 않았다. 왜냐하면 입력으로 사용되는 값이 ‘앞면’ 아니면 ‘뒷면’ 밖에 없어서 두 번만 대입해 보면 답을 알아낼 수 있기 때문이었다. 하지만 위의 소인수분해와 같이 입력값이 일반 숫자라면 모든 수를 다 대입해 볼 수는 없으므로 일방향함수를 미리 B에게 공개해도 무방하다.

1 2 3 4 5