보정 합산 알고리듬
카한이 보정 합산compensated summation 알고리듬을 고안하게 된 계기는, 미분방정식을 처리하는 과정에서 발견한 문제점 때문이었다. 컴퓨터를 사용하여 미분방정식의 해를 구할 때는 특정 구간을 정해 놓고 그 구간의 시작점에서부터 끝점까지 아주 조금씩 이동해 나가면서 근사치를 계산한다.
미분방정식 풀기는 마치 벌레가 조금씩 기어가는 식입니다… 각 스텝마다 버림rounding이 발생하기 때문에 결국은 오차가 계속 누적이 됩니다. 그래서 보정 합산 방식을 생각해 냈습니다.2
예를 들어, 컴퓨터가 다룰 수 있는 부동소수점 숫자가 소수점 2자리까지만 가능하다고 가정해 보자. 그럴 경우에 다음과 같은 수식을 계산하면 어떻게 될까?
![]() . 단,
. 단, ![]()
버림rounding이 없는 경우
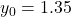
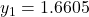
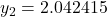
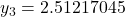
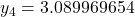
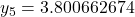 ...
...버림rounding이 있는 경우
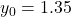
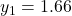
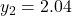
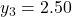
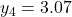
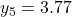 ...
...오차가 누적되는 것을 막기 위해서는 보정compensation이 필요하다. 만약, 버림rounding에 의해 버려지는 값을 그다음 단계의 계산에 반영해 줄 수 있다면 좋을 것이다. 그래서 카한은, 버려지는 오차를 저장하는 별도의 변수를 제안했다. 다음 단계의 합산에서 이 변수의 값을 사용하여 보정하면 오차가 누적되는 것을 막을 수 있다.
가드, 라운드, 스티키 비트
버림rounding의 영향을 최소화하기 위해서 카한은 세 개의 추가 비트를 제안했다. 이를 각각 가드guard, 라운드round, 스티키sticky 비트라고 부른다. 이는 어찌 보면 가수significand의 용량을 키운 것이다. 앞의 일화에서 TI 공학용 계산기가 눈에 보여주는 숫자는 최대 10자리이지만 실제 내부에서는 13자리 숫자를 사용하고 있는 것과 유사하다.

개념적으로 보자면 가드, 라운드, 스티키 비트는 부동소수점의 가수 부분 오른쪽에 나란히 놓인다. 그래서 가수 부분의 값이 오른쪽으로 시프트shift될 때# 가수 부분의 마지막 비트값이 가드 비트로 넘어가고 다시 시프트되면 가드 비트의 값은 라운드 비트로 넘어간다. 스티키 비트는 라운드 비트에서 넘어온 값이 1일 경우 1로 설정된 후 계속 1의 값으로 유지된다. 가드, 라운드, 스티키 비트가 어떤 장점을 가져오는지를 보여주는 예가 아래에 나와 있다. 편의상 가수significand 부분은 이진수로 표기했고, 가수 부분에는 3비트만 할당된다고 가정했다.
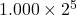 -
- 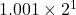 ------------
------------뺄셈을 위해서는 지수 부분을 동일하게 맞추어 주어야 한다. 그래서 지수 부분을 5로 맞추게 되면 다음과 같이 된다.
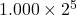 -
- 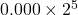 ------------
------------
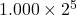
원래는 ![]() 이
이 ![]() 로 바뀌게 되는데, 가수 부분의 크기가 3비트이므로 소수점 넷째 자리 이하는 모두 날아가rounding 버린다. 만약 가수 부분의 크기에 제한이 없다면 다음과 같이 될 것이다.
로 바뀌게 되는데, 가수 부분의 크기가 3비트이므로 소수점 넷째 자리 이하는 모두 날아가rounding 버린다. 만약 가수 부분의 크기에 제한이 없다면 다음과 같이 될 것이다.
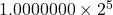 -
- 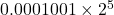 ------------
------------
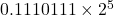 <- 부동소수점 규격에 맞추기 위해 왼쪽으로 시프트해야 함.
<- 부동소수점 규격에 맞추기 위해 왼쪽으로 시프트해야 함.
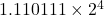 <- 소수점 아래 3자리를 맞추기 위해 반올림함.
<- 소수점 아래 3자리를 맞추기 위해 반올림함.
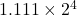
이제 가드, 라운드, 스티키 비트가 있는 경우에 어떻게 계산이 되는지 보자.
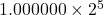 -
- 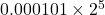 <- 가드 비트는 1, 라운드 비트는 0, 스티키 비트는 1
------------
<- 가드 비트는 1, 라운드 비트는 0, 스티키 비트는 1
------------
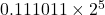 <- 부동소수점 규격에 맞추기 위해 왼쪽으로 시프트해야 함.
<- 부동소수점 규격에 맞추기 위해 왼쪽으로 시프트해야 함.
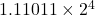 <- 소수점 아래 3자리를 맞추기 위해 반올림함.
<- 소수점 아래 3자리를 맞추기 위해 반올림함.
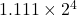
가드, 라운드, 스티키 비트를 사용하면, 가수 부분의 크기에 제한이 없는 경우와 같은 결과를 얻음을 볼 수 있다.
NaN
NaN은 Not a Number(숫자가 아님)의 약자이다. 그러면 이렇게 반문할지 모르겠다. “숫자가 아니면 문자인 거 아닌가요?” 이에 대한 답은 “아니요”이다. Not a Number를 정확하게 한국어로 표현한다면 “특정 숫자가 아님”이라고 하는 것이 더 맞을 듯싶다. 즉, 숫자이기는 한데, 딱 부러지게 정할 수 없는 경우를 의미한다. 다음과 같은 경우이다.
그리고, 연산에 NaN이 포함되면 그 결과는 무조건 NaN이다.
카한은 IEEE 754 표준을 정하는 과정에서 NaN을 제안했다.
점진적 언더플로우
어떤 저장 공간에 이 저장 공간이 허용하는 값보다 더 큰 값, 혹은 더 많은 값이 들어오면 결국 넘치는 정보는 사라지게 된다. 우리는 이런 현상을 오버플로우overflow라고 부른다. 언더플로우underflow는 너무 작은 값이 들어와서 정보가 사라지는 현상을 말한다.
부동소수점 연산에서 오버플로우와 언더플로우를 모두 경험할 수 있다. 둘 다 가수significand 부분의 크기가 한정되어 있기 때문에 발생한다. 예를 들어 가수 부분에 사용되는 비트가 4비트라고 가정해 보자. 그러면 가수 부분에 의해 표현될 수 있는 실제 가수 값은 1.0000 ~ 1.1111이 된다. 만약, 어떤 부동소수점 계산을 했더니 가수 값이 1.11111이 나왔다고 하자. 그러면 소수점 아래 5번째 자리의 수는 저장될 수 없으므로 버려진다. 이것이 오버플로우이다.
그런데 만약 계산의 결과가 0.000000001과 같이 아주 작은 값이라고 해보자. 일반적인 경우라면 이것을 정규화하게 되면 1.0 x 2-9 와 같이 변환해서 저장할 수 있지만, 지수 값을 마음대로 고칠 수 없는 상황이라면 결국 0의 값을 가수 부분에 저장해야 한다. 이런 경우를 언더플로우라고 한다.
카한은 IEEE 754 표준에 점진적 언더플로우gradual underflow를 제안했다. 이것은 쉽게 말하자면 정규화normalization 되지 않은 가수를 허용하는 것이다. 따라서 앞의 경우와 같이 0에 가까운 숫자를 직접 가수로 표현할 수 있게 된다.
부정확 알림 플래그
앞에서 우리는 부동소수점 연산 중 값의 일부를 버려야 하는 상황을 여럿 보았다. 결과적으로 우리는 정확한 값이 아니라 근사값을 구하게 된다. 그렇다면 이 값을 그대로 사용해도 무방할까? 그건 상황에 따라 다를 것이다.
그래서 카한은 부정확함을 알려주는 플래그를 추가하자고 제안했다. 만약 프로세서 내부에서 부동소수점을 처리하는 중에 오버플로우나 언더플로우가 발생하면 ‘부정확함inexact‘ 플래그를 1로 만든다. 프로그램의 계산 결과가 근사값인지의 여부는 이 플래그를 보면 알 수 있게 된다. 근사값을 허용할 수 없는 프로그램이라면 프로그래머는 이 ‘부정확함’ 플래그의 값을 반드시 확인해야 할 것이다.



답글 남기기