의사 난수 생성 알고리듬

난수random number는 규칙 없이 무작위로 만들어지는 숫자를 의미한다. 규칙 없이 만들어지는 숫자이므로 우리는 그 숫자를 높은 확률로 예측할 수 없다. 대표적인 것인 동전 던지기이다. 동전의 각 면이 나올 확률은 50퍼센트이다. 동전의 앞면을 ‘0’이라고 하고, 뒷면을 ‘1’이라고 정한 후에 8번을 던져서 그 결과를 이어 붙이면 이진수로 8비트의 수가 된다. 이렇게 만들어진 수는 높은 확률로 예측할 수 없으므로 난수이다.

그런데 컴퓨터로 난수를 만들어야 한다면 어떻게 될까? 컴퓨터는 알고리듬이 있어야만 무슨 일이든지 할 수 있다. 난수를 만들려면 난수를 만드는 알고리듬이 있어야 한다. 알고리듬으로 만들어진 난수는 무작위로 만들어졌다고 볼 수 있을까? 엄밀하게 따진다면 컴퓨터의 알고리듬이 만들어내는 난수는 진정한 난수가 아니다. 하지만, 그 난수를 예측하는 것이 불가능하다면 사실상 난수라고 볼 수 있다. 진정한 난수는 아니지만 사실상 난수를 지칭하는 용어가 의사 난수pseudo random number이다.

난수의 용도는 여러 가지가 있다. 그중 요즘 가장 실생활에서 접하기 쉬운 것은 OTP(One-Time Password)이다. 온라인으로 은행에서 거래할 때, 일회용 패스워드를 사용할 때가 많다. 이 패스워드는 사용 순간에 생성되는데, 사용자의 생성 장치에서만 확인이 가능하다. 만약 누군가 이 패스워드를 높은 확률로 예측할 수 있다면 보안은 유지되지 않을 것이다. 결국 OTP 생성기는 난수 발생기이다.

블럼은 의사 난수 생성에 관심이 많았다. 그가 생각하기에 무작위random하다는 것은, 계산복잡도가 굉장히 높다는 것이었다. <암호적으로 강력한, 의사 난수 비트열을 만드는 법​6​>에서는 주어진 숫자seed number에서 의사 난수 비트열sequence of pseudo random bits를 만드는 알고리듬을 제시했다. 이 알고리듬의 계산복잡도는 다항 시간polynomial-time에 가능했다. 즉, 빠른 시간 내에 처리가 가능하다는 의미이다. 그에 비해, 이미 주어진 비트값에서 다음 비트값을 예측해 내는 것은 이산 로그 문제discrete logarithm problem​11​와 동일한 계산복잡도를 가짐을 보였다. 이산 로그 문제는 일반 컴퓨터에서 계산하기 어려운 문제 중 하나이다. 블럼에게 난수란, 이미 만들어진 숫자를 보고 다음 숫자를 예측해 내는 계산복잡도가 너무 커서 현실적으로 컴퓨터로 계산할 수 없는 숫자인 셈이다.

<단순하고 예측 불가능한 의사 난수 발생기​7​>에서는 계산복잡도가 크다는 것만으로는 난수 발생기가 안전하지 않음을 보였다. 그는 아래의 두 가지 난수 발생 알고리듬을 비교했다.

  • 1/P
  • x^2 \ mod \ N

첫 번째는 이산 로그 문제에 기반하였고, 두 번째는 이차 잉여 문제quadratic residuosity problem​12​에 기반했다. 두 문제 모두, 다항 시간 내에 답을 낼 수 없는 어려운 문제로 알려져 있다. 하지만 블럼과 그의 연구팀은, 이산 로그 문제에 기반한 알고리듬의 경우, 난수 발생기의 입력값seed number을 유추해 냄으로써 난수 발생기의 다음 생성값을 찾아낼 수 있음을 알아냈다. 이에 비해 이차 잉여 문제에 기반하는 경우, 소인수분해 계산이 포함되어 있어서 다음 생성값을 현실적으로 예측하기 어렵다.

공개키 암호화

암호화encryption는, 정보가 적에게 노출되더라도 그 내용이 드러나지 않도록 하기 위함이다. 하지만 동시에 우리 편의 손에 넘어갔을 때는 그 내용이 쉽게 확인되어야 한다. 컴퓨터 과학의 관점에서 보면, 암호화는 데이터의 변환이다. 변환된 데이터를 원래의 데이터로 복원하는 방법은 특정 값key을 이용하며, 그 값을 모르면 복원하기 어려워야 한다. 여기서 어렵다는 말은 계산복잡도가 매우 커서 현실적으로 너무 긴 시간이 걸린다는 의미이다.

계산복잡도에 관심이 많던 블럼에게 암호학은 매우 매력적인 분야였음에 틀림없다. <모든 조각 정보를 감춘, 효율적인 확률형 공개키 암호화 방법​8​>에서 그는 완벽한 정보 봉쇄를 꿈꿨다. 1970년대 후반에 디피-헬만 키 교환, RSA 암호화 같은 공개키 암호화 방법이 발표되면서 큰 주목을 받았다. 이런 암호화 방법은 소인수분해와 같이 계산복잡도가 매우 큰 계산을 도입하여 암호 해독이 현실적으로 거의 불가능하게 만들었다.

그런데 블럼은 이런 암호화 방법이 원본 정보를 보호하는 데는 성공했지만, 완벽하게 모든 정보를 통제하지는 못함을 발견했다. 그는 RSA와 같은 결정적 공개키 암호화deterministic public-key encryption 방식이 확률적 공개키 암호화probabilistic public-key encryption에 비해 암호화나 복호화 속도가 빠르기는 하지만, 적에게 유의미한 조각 정보를 노출할 수도 있음을 확인했다. 결정적 공개키 암호화는 같은 입력에 대해 항상 같은 결과값이 나오는 반면에, 확률적 공개키 암호화는 암호화를 할 때마다 다른 결과값이 나올 수 있다. 그런 점에서 확률적 공개키 암호화가 더 안전하다고 볼 수 있으나, 대신에 암호화와 복호화의 시간이 상대적으로 더 걸렸다. 블럼과 골드와서는 의사 난수 발생기를 도입해서, 기존의 결정적 공개키 암호화에 확률적 암호화 기법을 접목시켰다. 이를 통해서 효율은 결정적 공개키 암호화처럼 높지만, 확률적 암호화처럼 정보 유출을 최대한 막을 수 있었다.

프로그램 검사

소프트웨어 프로그램이 정확하게 동작하는지를 자동으로 확인하는 방법이 있다면 좋을 것이다. 그래서 일찍부터 그런 방법을 찾으려는 노력이 있었다. 프로그램 코드를 수학적으로 모델링한 후에, 수학적 증명 방법을 적용하는 것이 대표적인 사례였다. 로버트 플로이드와 토니 호어의 연구가 대표적이다.

이에 비해 블럼의 방식은 ‘증명verification‘이라기 보다는 ‘검사checking‘에 가깝다. 수학적 모델링으로 수식을 만드는 것이 아니라, 여러 입력값들을 프로그램에 넣어 보면서 그 결과가 예상과 같은지를 확인하는 식이다. <자신의 작업을 검사하는 프로그램 설계하기​9​>에서 ‘프로그램 검사기program checker‘라는 개념을 소개했다. 이 프로그램 검사기가 하는 일은, 주어진 문제(\pi)와 이 문제를 위해 만들어진 프로그램(P)를 놓고 입력에 대해 출력이 동일한지를 확인하는 일이다. 하지만 모든 입력을 일일이 다 검사할 수는 없으므로, 효율적으로 입력을 모델링할 필요가 있다.

블럼은 몇 가지 유형의 문제들에 대해 프로그램 검사기의 알고리듬을 제시했다. 그중 정렬sorting 문제에 대한 프로그램 검사기 알고리듬은 다음과 같다.

<문제>
입력: 정수 배열 X =[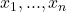x_1, ..., x_n]
출력: X의 원소를 올림차순으로 배열한 Y
<검사기>
입력: 두 개의 배열 X = [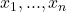x_1, ..., x_n], Y = [y_1, ..., y_n]
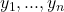출력: 만약 Y의 원소가 올림차순이 아니거나 X와 Y의 원소가 일치하지 않으면 "버그 있음".
     만약 작성한 정렬 프로그램의 정확하고 정렬을 하면 "정확함".

블럼은 프로그램 검사기 알고리듬이 검사 대상이 되는 프로그램 보다 계산복잡도가 높지 않음을 증명했다.

1 2 3 4 5