튜링상 관련 업적
수치해석에 근본적인 기여를 했다. 부동소수점 계산에 관한 가장 중요한 전문가 중 한 명이다. 그는 “이 세상이 수치 계산으로부터 안전하도록 만드는 데” 헌신했다.
1989년 튜링상 선정 이유4
윌리엄 카한은 튜링상 수상 강연을 하지 않았다. 그 이유는 알려진 바가 없다. 그저 추측을 해보자면, 본인에게 너무 과분한 상이라고 생각했거나 혼자서 모든 공을 차지하기가 미안해서가 아닐까 한다. 그는 인터뷰에서 다음과 같이 언급했다.
공동 연구자를 잘 택하고 기회를 잘 잡아 정말로 값어치 있는 일을 해낼 수 있었던 나는 참 운이 좋았다고 말하고 싶네요. 하지만 나 혼자만의 힘으로 했던 것은 아닙니다. 이런 상을 받았을 때 “이 사람은 영웅이야. 그는 모든 것을 혼자서 해냈어”라는 식으로 보여서 안타깝습니다… 나는 그 일이 벌어졌을 때 중심부에 가까이 있었습니다. 하지만 그렇다고 그 일을 혼자서 했던 것은 아닙니다.2
숫자를 온전히 다루지 못하는 컴퓨터의 운명
컴퓨터는 숫자를 다루기 위해 태어났다. 하지만 안타깝게도 컴퓨터는 숫자를 온전하게 다루지 못할 운명을 타고났다. 숫자는 크기가 무한한 추상적 객체인 반면에, 컴퓨터는 크기에 한계가 있는 현실적 존재이기 때문이다.
예를 들어 우리는 연필과 종이와 두뇌를 가지고 10의 1,000제곱인 정수(101000)를 다룰 수 있다. 하지만 일반적인 64비트 컴퓨터에서는 최대로 다룰 수 있는 정수의 크기가 10의 20제곱(1020)보다 작다. 컴퓨터는 숫자를 표현하는 비트bit의 개수에 제한이 있기 때문이다. 64비트 컴퓨터라고 부를 때는 그 컴퓨터가 다룰 수 있는 데이터의 최대 크기가 64비트라는 의미이다. 이렇게 되면 이 컴퓨터가 표현할 수 있는 정수의 최대값은 264 – 1 이다. (만약 부호를 위해 한 개의 비트를 사용한다면 최대 정수값은 더 작아진다.)
실수는 정수보다 더 골치 아프다. 쉽게 생각하자면 실수란 소수점이 있는 숫자이다. 12.345라는 숫자를 컴퓨터에서는 어떻게 표현해야 할까? 소수점 위의 숫자 12와 소수점 아래의 숫자 345를 분리해서 다뤄야 할까? 아니면 그냥 12345를 저장하고 항상 소수점 아래 숫자는 3자리라고 가정해 버릴까?
초기의 전자식 컴퓨터가 탄도 계산 및 편미분방정식 계산에 사용되었음을 상기하자. 이런 수식 계산은 모두 실수를 사용한다. 따라서 실수를 어떻게 다루어야 할지는 전자식 컴퓨터의 초기 시절부터 중요한 사항이었다. 하지만 의외로 이 부분은 오랜 기간 동안 간과되어 왔다.
전자식 컴퓨터의 기본 구조를 확립했던 존 폰 노이만조차도 실수 계산을 수학자들의 재량에 맡겨 버렸다. 아마도 그는 컴퓨터가 극소수의 과학자와 수학자들 사이에서만 사용될 것으로 단정 지었던 듯싶다.
폰 노이만은 컴퓨터에서 다루는 숫자는 모두 소수점 이하의 값이라고 가정해 버렸다. 예를 들어 원래 다뤄야 할 숫자가 12.345라고 한다면, 컴퓨터 프로그램에서는 12345로 표현하고 이 값은 소수점 이하의 값이라고 간주한다. 이렇게 되면 실제 숫자보다 100분의 1로 축소된 값이 사용되는 셈이 된다.
축소scale-down는 그 프로그램이 다루어야 할 모든 숫자들에 일괄적으로 적용된다. 예를 들어, 프로그램에서 다루어야 하는 숫자가 12.345 외에 5.67, 789.123 등이 있다면 789.123을 0.789123으로 만들기 위해서 모든 숫자를 1,000분의 1로 축소한다. 그렇게 되면 0.012345, 0.00567, 0.789123과 같은 식으로 바뀌게 될 터인데 소수점 아래의 길이를 맞추면 0.012345, 0.005670, 0.789123이 될 것이다. 그러면 이제 소수점을 날려버리고 소수점 아래에 있는 숫자를 프로그램 내에서 정수처럼 사용한다. 12345, 5670, 789123을 사용해서 프로그램을 작성하는 것이다. 프로그램이 수행되어 정수값으로 결과가 나오면 이제 역순으로 숫자를 변환한다. 예를 들어, 결과값으로 87456라는 값이 구해진다면 이 값은 실제로는 소수점 아래 여섯 자리 값이어야 하므로 0.087456로 해석되고 원래값에서 1,000분의 1로 축소되어 계산된 결과이므로 1000을 곱해서 87.456이라는 최종값을 얻게 된다.
부동소수점 연산
컴퓨터에서 실수를 제대로 표현하기 위해 고안한 방식이, 부동소수점floating-point 이다. 이 방식은 지수exponent와 가수significand를 사용한다. (가수를 영어로는 mentisa 혹은 fraction이라고도 부른다.) 아래에 예가 나와 있다.
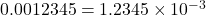
위의 예에서 12345가 가수significand에 해당하고 -3이 지수exponent에 해당한다. 10은 밑base이라고 부른다. ‘부동소수점’이라는 표현이 사용된 이유는 ‘고정소수점fixed-point‘이라는 방식과 구별하기 위함이다. 고정소수점이란 컴퓨터에서 다루는 숫자들이 항상 정해진 소수점 위치를 가지는 방식이다. 앞에서 폰 노이만이 사용했던 방식이다. 폰 노이만의 방식에서는 프로그램에 있는 실수들이 모두 소수점 바로 밑에 있는 숫자라고 간주되었다. 하지만 부동소수점 방식은 소수점이 어디에 오건 간에 컴퓨터 프로그램에서 모두 표현할 수 있기 때문에 ‘fixed’와 구별하기 위해 ‘floating’이라는 표현을 사용했다.¶
부동소수점 방식이 처음 등장한 것은 20세기 초였다. 그리고 1938년에 독일의 콘라드 추세Konrad Zuse가 만든 기계식 컴퓨터 Z1이 부동소수점 연산을 지원했다. 본격적으로 부동소수점 연산이 대중화되기 시작한 것은 IBM 704 모델부터였고 과학계산용 컴퓨터에서만 주로 사용되었다.
과학계산용 컴퓨터는 특정 용도에 한정되어 사용되었기 때문에 굳이 호환성을 신경 쓸 필요는 없었을 것이다. 오히려 성능을 높이기 위해서라면 호환성을 과감히 포기하는 편이었다. 그렇기 때문에 부동소수점 연산을 위한 표준은 큰 쟁점으로 부각되지 않았다. 그러다 보니 부동소수점을 표현하기 위한 가수, 지수, 밑의 크기가 제조사 별로 달랐다. 예를 들어 CDC의 컴퓨터에서 작성한 부동소수점 연산 프로그램용 실수real number 데이터들은 DEC의 컴퓨터에서 바로 사용할 수 없었다.


부동소수점의 장점은 매우 큰 수와 매우 작은 수를 모두 표현할 수 있다는 점이다. 이제 64비트 컴퓨터에서도 101000을 다룰 수 있다. 하지만 여전히 문제는 있다. 가수significand의 크기는 여전히 제약되어 있다. 위의 그림에서 VAX-11 컴퓨터는 가수에 사용되는 최대 비트 개수가 23개이다. 이진 부동소수점binary floating-point 구조를 사용한다고 가정한다면 다음과 같은 수는 표현할 수 없다.
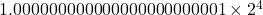
위의 표현에서 주의할 점은 이진수와 십진수 표기가 섞여 있다는 것이다. 숫자 2, 4는 십진수이다. 밑이 2임을 알리기 위해 십진수 표기를 그대로 썼다. 하지만 가수 부분은 이진수 표기이다. VAX-11 컴퓨터의 포맷에 대응시키기 위해 이진수 표기를 사용했다.
그리고, 가수 부분에 오는 값은 항상 소수점 아래 자리이다. 마치 폰 노이만이 사용했던 방식과 유사해 보이는데 두 가지 차이점이 있다. 먼저 소수점 앞에 0이 있는 것이 아니라 1이 있다. 즉, 부동소수점 포맷의 가수 부분에 ![]() 라는 값이 온다면 실제 가수값은
라는 값이 온다면 실제 가수값은 ![]() 인 것이다. 이를 정규화normalization이라고 부른다. 만약,
인 것이다. 이를 정규화normalization이라고 부른다. 만약, ![]() 라는 실수를 부동소수점 포맷으로 바꾼다면, 일단 정규화를 해서
라는 실수를 부동소수점 포맷으로 바꾼다면, 일단 정규화를 해서 ![]() 로 만든다. 그러면
로 만든다. 그러면 ![]() 이 부동소수점 포맷의 가수 부분에 들어가고
이 부동소수점 포맷의 가수 부분에 들어가고 ![]() 가 지수 부분에 들어간다. (편의상 밑과 지수는 십진수로 표기했다.)
가 지수 부분에 들어간다. (편의상 밑과 지수는 십진수로 표기했다.)
위의 예에 나온 숫자를 VAX-11의 부동소수점 포맷에 맞춘다면 소수점 아래에 있는 이진수 ![]() 값을 가수로 사용하게 되고 4(이진수 100)를 지수로 사용하게 된다. 그런데 이진수
값을 가수로 사용하게 되고 4(이진수 100)를 지수로 사용하게 된다. 그런데 이진수 ![]() 은 3비트이므로 문제가 없지만 이진수
은 3비트이므로 문제가 없지만 이진수 ![]() 는 총 24비트이어서 결국 가장 오른쪽 비트를 버려야 하는 문제가 발생한다. 그렇게 되면 결국 VAX-11 컴퓨터에서는 이 값이
는 총 24비트이어서 결국 가장 오른쪽 비트를 버려야 하는 문제가 발생한다. 그렇게 되면 결국 VAX-11 컴퓨터에서는 이 값이
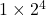
처럼 되어 버려서 실제 값과는 오차가 생겨 버린다.



답글 남기기