튜링상 관련 업적
수치해석법, 자동 코딩 시스템, 오류 검출 및 정정 코드에서의 업적
1968년 튜링상 선정 이유
오류 검출 및 정정 코드 (Error Detection & Correction Code)
흔히 우리는 “컴퓨터처럼 정확하다”라는 표현을 쓰곤 한다. 컴퓨터로 계산한 결과를 신뢰하기 때문이다. 하지만 초기의 컴퓨터는 그렇게 신뢰할만한 기계가 아니었다. 아주 빠르게 계산을 하기는 했지만 틀릴 수도 있는 기계였다. 그도 그럴 것이, 가장 중요한 부품이었던 진공관부터가 그리 신뢰할만한 물건이 아니었다. 또한, 천공테이프punched tape와 같이 기계적 동작을 하는 요소들은 환경의 변화나 작업자의 실수에 의해서 오동작할 가능성이 있었다. 오늘날 컴퓨터가 이렇게 신뢰의 상징이 될 수 있었던 데에는 반도체의 힘이 크다고 보아도 무리는 아닐 듯싶다. 초기 컴퓨터의 불안정성은 최근 태동하고 있는 양자 컴퓨터에서 엿볼 수 있다.
과학자들은 컴퓨터의 빠른 계산 속도에 매료되었기 때문에 어떻게든 컴퓨터의 신뢰성을 높여보려고 노력했다. 설계 단계에서부터 신뢰성을 높이는 기법을 적용함은 물론이었고, 운용 중에 발생할 수 있는 상황적 오작동도 피하고 싶었다. 그래서 나온 것이 데이터의 오류를 검출하는 기법이다. 대표적인 예가 패리티Parity 비트이다. 이진수로 표현된 코드에서 1의 값을 가지는 비트의 개수를 짝수(혹은 홀수)로 유지하도록 추가 비트를 첨부하는 방식이다.
0010 -> 00101
0110 -> 01100위의 예는 짝수 패리티 비트를 보여준다. 4개의 비트로 구성된 코드값에서 1의 값을 가지는 비트의 개수가 홀수이면 1을 추가하고 짝수이면 0을 추가한다. 이렇게 하면 5개의 비트에서 1의 값을 가지는 비트의 개수가 짝수개가 된다.
따라서, 컴퓨터가 천공테이프에서 데이터를 읽어올 때 00001이라는 값을 발견한다면 1의 값을 가지는 비트가 1개, 즉 홀수개이므로 뭔가 오류가 생겼음을 알게 된다(즉, 검출하게 된다). 이렇게 오류가 검출되면 컴퓨터는 진행을 중단하고 뭔가 조치를 취해야 한다. 가장 대표적인 조치는 재시도하는 것이다. 만약 천공테이프에서 구멍을 감지하는 센서에 잠깐 파리가 앉았었다고 하면 그다음 재시도에서는 오류 없이 통과할 가능성이 높다. 하지만 천공테이프의 구멍이 완벽하게 뚫리지 않았기 때문에 생겼던 문제라면 재시도해도 오류가 검출될 것이다. 몇 번의 재시도에도 오류가 사라지지 않는다면 컴퓨터는 더 이상 작업을 진행하지 않고 중단한다.
이것이 바로 리처드 해밍이 어느 월요일 아침에 뉴욕시 컴퓨터 센터에서 마주한 상황이었다.†† 그가 겪었던 오류의 원인이 무엇이었는지는 알려지지 않지만, 두 번이나 같은 일을 겪은 이 총명한 젊은 수학자는 엄청나게 열받았음이 분명했다.
이 문제를 해결하고 싶었던 해밍의 첫 번째 아이디어는 고전적인 투표 방식이었다. 그는 이미 오류 검출에 관한 프로젝트에 참여한 경험이 있었다. 그 프로젝트에서는 같은 회로를 3개 만들어서 3개의 결과를 비교했다. 3개의 결과가 일치하지 않을 때는 2개가 일치한 결과를 사용하는 식이었다. 오류가 발생해도 올바른 결과를 찾아서 작업을 계속 진행할 수 있기는 했지만 해밍이 처한 상황에는 적용이 불가능했다. 그렇게 하려면 그 비싼 컴퓨터를 두 대 더 할당받아야 하기 때문이었다.
그래서 해밍은 코딩 방식에 주목했다. 오류가 발생하면 어느 비트에 오류가 생겼는지를 꼭 집어낼 수 있게 만들 방법은 없을까? 해밍은 이 질문에 답을 찾아가는 과정에 대해 비교적 소상하게 설명한 바가 있다.5
첫 시작은 2차원 좌표를 만드는 것이었다. 예를 들어 0010010101101010 이라는 16비트 데이터가 있다고 해보자. 이것을 쪼개서 아래와 같이 2차원으로 배치한 후에 X축 방향과 Y축 방향으로 각각 패리티 비트를 만드는 식이다. 아래의 예에서는 짝수 패리티를 가정했다. 아울러 가로 방향을 먼저 한 후에 세로 방향을 진행했다.

이제 어떤 비트에서 오류가 발생하면 X축 방향과 Y축 방향으로 각각 패리티 에러가 발생하게 되고 자연스럽게 해당 비트의 좌표를 얻게 된다. 그런데 해밍은 여기서 멈추지 않았다. 그는 과연 이것이 최선의 방법인지 자문해보았다. 패리티 비트의 개수를 줄일 수 있다면 더 좋을 것이다. 그래서 생각해낸 것이 차원을 늘리는 것이었다. 만약 3차원으로 배치한다면 어떨까?

이제 X, Y, Z 축이 각각 패리티 비트를 가지게 되는데 위의 예에서 x1이라는 패리티 비트의 값은 회색으로 표시된 평면에 위치한 모든 데이터들을 사용해서 계산된다. 이제 어떤 비트에서 오류가 발생하면 X, Y, Z 축 방향으로 각각 패리티 에러가 발생하면서 해당 위치의 좌표를 알 수 있게 된다.
해밍은 계속 차원을 증가시켜 보았고, 결국 최종적으로 2x2x…x2까지 차원을 증가시킬 수 있음을 깨달았다.(왜냐하면 하나의 축에는 최소한 한 개의 정보 비트와 한 개의 패리티 비트가 있어야 하기 때문이다.) 만약 이때의 차원이 n차원이라고 한다면 필요한 패리티 비트의 개수는 n+1이 된다.
그렇다면 이것이 최선일까? 그렇지 않았다. 오히려 반대였다. 위의 예에서 전체 비트 중 정보 비트는 n개이고 패리티 비트는 n+1이 되므로 오히려 배보다 배꼽이 더 커지는 셈이 된다. 그리고 n+1개의 패리티 비트가 나타낼 수 있는 좌표의 개수는 총 2n+1개이지만 실제로 존재하는 비트의 개수는 2n이므로 큰 낭비가 발생하고 있었다.
해밍이 머리 힐에서 뉴욕시까지 회사의 우편 배달 버스를 타고 가며 골똘히 생각에 빠진 때가 바로 이 시점이었다. 그는 이 문제를 해결할 방법이 무엇이 있을까 골몰하였고 마침내 며칠 후에 해결책을 생각해냈다. 그는 신드롬syndrome이라는 개념을 고안했다. 신드롬은 앞의 방법과 마찬가지로 원래의 정보 비트 값에 덧붙이는 추가 비트이고, 오류가 발생할 경우 오류가 발생한 위치를 알려주는 역할을 한다. 앞에서의 방법과 차이점이라면 1차원상에서 구현된다는 것이다. 따라서 1번째 비트에 오류가 발생하면 신드롬의 값이 1이 되어야 하고 4번째 비트에 오류가 발생하면 신드롬의 값은 4가 되어야 한다. 7개의 비트로 구성되는 코드에서 가능한 신드롬의 값은 아래와 같을 것이다.
오류 위치 신드롬 값
1 001
2 010
3 011
4 100
5 101
6 110
7 111그렇다면, 신드롬의 최하위 비트는 코드의 1번, 3번, 5번, 7번 비트 중 하나에 오류가 발생할 때 1의 값을 가지면 된다. 신드롬의 최상위 비트는 코드의 4번, 5번, 6번, 7번 비트 중 하나에 오류가 발생할 때 1의 값을 가지면 된다. 마찬가지로 신드롬의 가운데 비트는 코드의 2번, 3번, 6번, 7번 비트 중 하나에 오류가 발생할 때 1의 값을 가지면 된다.
다시 말하자면 신드롬의 최하위 비트는 코드의 1번, 3번, 5번, 7번 비트에 대해 패리티 검사를 한 결과인 셈이다. 만약 어느 한 비트에 오류가 생기면 패리티 검사에서 오류가 생길 것이다.(즉 결과값이 1로 나타난다는 의미이다.)
신드롬이 3비트이면, 오류가 발생하지 않을 때를 제외하여 총 7개의 오류 위치를 구별할 수 있다. 즉 7비트의 코드를 지원할 수 있다. 그런데 주의할 점이 있다. 신드롬 값은 검사를 위해 항상 관련 정보 비트들과 함께 붙어 다녀야 한다. 따라서 7비트 중 신드롬 값이 3비트를 차지하게 되며 결국 일반 정보용으로는 4비트만 사용이 가능하다.
신드롬 값의 각 비트를 계산할 때는 오직 정보 비트만이 사용되어야 하므로 이를 고려하여 신드롬 비트를 배치하면 아래의 그림과 같다. 이런 방식으로 만든 코드를 해밍 코드Hamming Code라고 부른다.
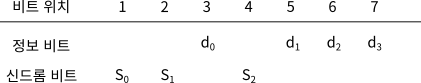
위의 해밍 코드에서 각 신드롬 비트를 계산하는데 사용되는 정보 비트는 다음과 같다.
S0 : d0 d1 d3
S1 : d0 d2 d3
S2 : d1 d2 d3


답글 남기기