오차해석
이제 우리는 오차해석이 왜 필요한지를 알게 되었다. 컴퓨터가 숫자를 온전하게 표현하지 못함으로 인해 생기는 문제였다. 수식 계산에 있어서 온전하지 못한 숫자를 입력으로 사용해서 계산하게 되면 당연히 결과값도 정답과 차이가 생길 수밖에 없다. 아래의 예를 보자.
![]()
위와 같은 계산을 해야 하는데 ![]() 값으로
값으로 ![]() 가 주어졌다고 하면, 수학의 세계에서는 다음과 같이 계산된다.
가 주어졌다고 하면, 수학의 세계에서는 다음과 같이 계산된다.
![]()
우리는 굳이 ![]() 를 따로 계산하지 않고 기호를 이해하여 문제를 푼다.
를 따로 계산하지 않고 기호를 이해하여 문제를 푼다.
하지만 컴퓨터의 세계에서는 ![]() 에 값(숫자)을 주어야지 기호를 줄 수가 없다. 따라서
에 값(숫자)을 주어야지 기호를 줄 수가 없다. 따라서 ![]() 의 값을 계산해야 한다. 그런데 잘 알려졌다시피 그 값은 소수점 아래의 수가 무한대로 이어지는 무한소수이다. 어떤 컴퓨터를 가져다 놓아도 그 값을 완벽하게 표현할 수 없다. 결국은 반올림 오차가 발생한다. 여기서는 그냥 예로 소수점 아래로 6자리까지만 저장 가능하다고 하자. 그러면 1.41421라는 값으로 근사되며
의 값을 계산해야 한다. 그런데 잘 알려졌다시피 그 값은 소수점 아래의 수가 무한대로 이어지는 무한소수이다. 어떤 컴퓨터를 가져다 놓아도 그 값을 완벽하게 표현할 수 없다. 결국은 반올림 오차가 발생한다. 여기서는 그냥 예로 소수점 아래로 6자리까지만 저장 가능하다고 하자. 그러면 1.41421라는 값으로 근사되며 ![]() 에 1.41421이 치환되어 다음과 같은 결과를 가져온다.
에 1.41421이 치환되어 다음과 같은 결과를 가져온다.
![]()
원래 정답은 2이지만 컴퓨터가 계산한 값은 1.999899241이므로 0.000100759만큼의 오차가 발생했다. 이 예에서는 소수점 아래로 6자리까지만 저장하는 컴퓨터라고 했으므로 실제로 최종 저장하는 값은 1.999899이며 따라서 오차는 0.000101이 된다.
이 결과를 받아들여야 할 것인가? 말 것인가? 이는 주어진 상황에 달려있다. 0.000101의 오차를 무시할 수 있는 응용이라면 받아들여야 하고 그렇지 않다면 버려야 한다.
순방향 오차해석
위의 예에서 우리는 계산 결과값을 구한 후 그것을 정답과 비교하여 오차의 크기를 따져보았다. 이렇게 입력값을 주고 계산을 한 후에 결과값의 오차를 따지는 방식을 순방향 오차해석이라고 한다. 상식적인 방법이지만 순방향 오차해석에는 문제가 있다. 내가 정답을 확실하게 알고 있어야 한다는 것이다. 그래야만 얼마나 오차가 생겼는지를 따져볼 수 있을 것이다. 하지만 정답을 확실히 알고 있다면 뭐 하러 컴퓨터로 힘들게 계산을 하겠는가? 따라서 앞의 예와 같은 오차해석은 실제로 벌어지기 어렵다.
윌킨슨이 12개짜리 방정식을 풀었을 때, 그는 12개의 변수값을 모두 구했지만 그 값들이 얼마나 정확한지 확신하지 못했다. 그저 마지막 단계에서 사용된 숫자들에서 6자리까지만 유효값이 있는 것을 보고, 최종 계산된 변수값들도 6자리까지만 유효하리라 추측했을 뿐이었다. 하지만 반전이 있었다. 12개의 변수값을 방정식에 대입해보니 완벽하게 오차 없이 맞아떨어진 것이다.
그는 12개짜리 방정식을 풀기 위해서 12×12 크기의 행렬 연산을 했다. 그는 가우스 소거법을 적용하면서 부분 피벗팅Partial Pivoting 방식을 썼다. 만약 GEPP(Gauss Elimination Partial Pivoting) 방식의 계산으로 구한 결과값이 정답과 별로 오차가 없다는 것이 증명되어 있었다면 그렇게 마음 졸이면서 계산하지는 않았을 것이다.
계산기를 사용한 행렬 연산의 결과물을 얼마나 신뢰할 수 있을지에 대해서 당시에는 비관적인 견해가 대세였다. 윌킨슨이 국립물리연구소에서 18개까지 방정식을 접했을 때 앨런 튜링이 보여준 반응을 보면 당시의 분위기를 엿볼 수 있다. 가우스 소거법은 이미 계산된 결과에 다시 계산을 하는 단계가 반복되므로 오차가 계속 증폭되리라고 추측한 것이 당연했을 것이다.
그리고 행렬 연산의 오차해석에 관한 초창기 논문은, 결과값의 오차가 최대 ![]() 에 달할 것이라는 아주 비관적인 결론을 내리고 있었다.9 물론 오차가 실제로는 훨씬 작을 수도 있었지만 최악의 경우는
에 달할 것이라는 아주 비관적인 결론을 내리고 있었다.9 물론 오차가 실제로는 훨씬 작을 수도 있었지만 최악의 경우는 ![]() 이라는 것이었으므로 그 누구도 섣불리 행렬 연산의 결과를 안심하고 쓸 수 없었다. 국립물리연구소에서 18개 방정식을 풀고 난 후에 앨런 튜링은 그 결과값이 정확한 것에 충격을 받고, 이에 관한 연구를 해서 논문을 발표하기도 했다. 그는 최대 오차가
이라는 것이었으므로 그 누구도 섣불리 행렬 연산의 결과를 안심하고 쓸 수 없었다. 국립물리연구소에서 18개 방정식을 풀고 난 후에 앨런 튜링은 그 결과값이 정확한 것에 충격을 받고, 이에 관한 연구를 해서 논문을 발표하기도 했다. 그는 최대 오차가 ![]() 수준일 것이라고 계산했다.
수준일 것이라고 계산했다.
아무튼 행렬 연산의 결과값을 얼마나 신뢰할 수 있을지에 대해 순방향 오차해석에 관한 연구는 큰 도움을 주지 못하고 있었다.
역방향 오차해석
역방향 오차해석은 계산 결과의 오차에 관심을 두지 않는다. ‘역으로’ 생각해서, 결과값을 만들어 내는 입력 데이터의 오차 범위에 관심을 둔다. 순방향 오차해석과 역방향 오차해석의 차이를 보여주는 대표적인 그림이 다음과 같다.
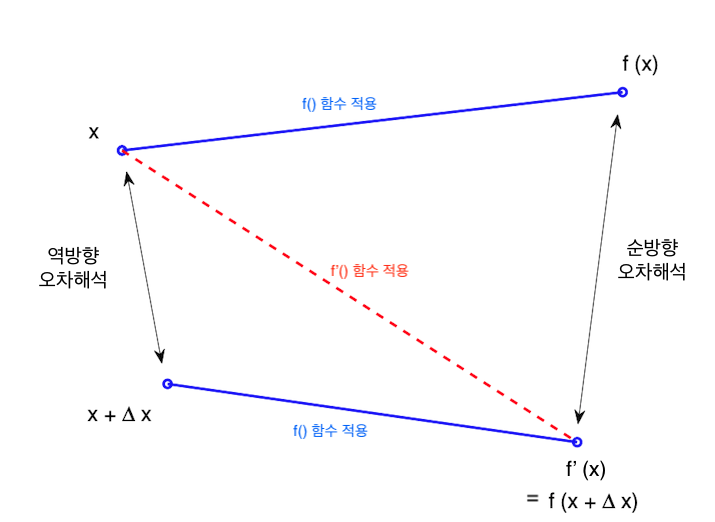
그림을 해석해보자. ![]() 라는 입력 데이터를 사용해서
라는 입력 데이터를 사용해서 ![]() 라는 계산 결과를 구하는 것이 목표이다.
라는 계산 결과를 구하는 것이 목표이다. ![]() 는 완전히 수학의 세계에서 계산한 결과, 즉 정답이다. 하지만 컴퓨터를 사용해서 계산하면 오차가 발생한다. 컴퓨터를 사용한 계산은
는 완전히 수학의 세계에서 계산한 결과, 즉 정답이다. 하지만 컴퓨터를 사용해서 계산하면 오차가 발생한다. 컴퓨터를 사용한 계산은 ![]() 이다.
이다. ![]() 은
은 ![]() 를 컴퓨터의 알고리즘으로 구현한 것을 말하며
를 컴퓨터의 알고리즘으로 구현한 것을 말하며 ![]() 와
와 ![]() 는 같을 수도 있고 다를 수도 있다. 둘 사이의 차이가 순방향 오차에 해당한다. 그리고 이 오차가 얼마나 될지를 조사하는 것이 순방향 오차해석이다.
는 같을 수도 있고 다를 수도 있다. 둘 사이의 차이가 순방향 오차에 해당한다. 그리고 이 오차가 얼마나 될지를 조사하는 것이 순방향 오차해석이다.
그런데, 약간 발상의 전환을 해보자. 컴퓨터로 계산한 ![]() 의 값과 동일한 결과를 내는
의 값과 동일한 결과를 내는 ![]() 이 있을 수 있다. 즉 수학의 세계에서 계산했을 때, 컴퓨터의 세계에서 계산한 결과값과 동일한 값을 만들어내는 상황을 상상하는 것이다. 그리고 수학의 세계에서 이런 결과를 만들어 내는 입력 데이터를
이 있을 수 있다. 즉 수학의 세계에서 계산했을 때, 컴퓨터의 세계에서 계산한 결과값과 동일한 값을 만들어내는 상황을 상상하는 것이다. 그리고 수학의 세계에서 이런 결과를 만들어 내는 입력 데이터를 ![]() 이라고 한다면
이라고 한다면 ![]() 이
이 ![]() 와 같을 수도 있고 다를 수도 있다. 그 차이를
와 같을 수도 있고 다를 수도 있다. 그 차이를 ![]() 라고 하면
라고 하면 ![]() 인 셈이다.
인 셈이다.
만약 ![]() 가 0이라면 더 이상 왈가왈부할 이유가 없다.
가 0이라면 더 이상 왈가왈부할 이유가 없다. ![]() 인 셈이 되므로 결국 컴퓨터가 구한 결과는 원래 구하려던 정답과 동일하다. 그런데
인 셈이 되므로 결국 컴퓨터가 구한 결과는 원래 구하려던 정답과 동일하다. 그런데 ![]() 가 0이 아니라면 어떻게 되나?
가 0이 아니라면 어떻게 되나? ![]() 가 아주 작다면, 결과에 별 영향을 주지 못할 정도로 작다면 어떻게 되나? 결과에 별 영향을 주지 못할 정도로 작다는 의미는 그
가 아주 작다면, 결과에 별 영향을 주지 못할 정도로 작다면 어떻게 되나? 결과에 별 영향을 주지 못할 정도로 작다는 의미는 그 ![]() 를 사용한 계산을 답으로 받아들여도 된다는 의미 아니겠는가? 그러므로 우리는
를 사용한 계산을 답으로 받아들여도 된다는 의미 아니겠는가? 그러므로 우리는 ![]() 의 값을 답으로 인정해도 된다.
의 값을 답으로 인정해도 된다.
역방향 오차해석은 바로 ![]() 의 크기를 찾고 그 크기가 무시할 수 있는 수준인지를 판단하는 것이다. 무시할 수 있는 수준인지 판별하는 기준으로 섭동이론perturbation theory이 사용되었다. 섭동이론이란, 어떤 계산에 있어서 입력값의 변동이 어느 수준까지 계산 결과에 영향을 주는지를 따져보는 이론이다.10
의 크기를 찾고 그 크기가 무시할 수 있는 수준인지를 판단하는 것이다. 무시할 수 있는 수준인지 판별하는 기준으로 섭동이론perturbation theory이 사용되었다. 섭동이론이란, 어떤 계산에 있어서 입력값의 변동이 어느 수준까지 계산 결과에 영향을 주는지를 따져보는 이론이다.10
이제 윌킨슨의 연구 결과를 살펴보자. 그는 가우스 소거법을 사용하여 다음의 행렬식을 분석했다.
![]()
![]() 와
와 ![]() 의 값이 주어지고
의 값이 주어지고 ![]() 라는 벡터값을 구하는 경우이다. 윌킨슨은 Partial pivoting이나 Complete pivoting을 사용할 때에 다음을 만족함을 보였다.11
라는 벡터값을 구하는 경우이다. 윌킨슨은 Partial pivoting이나 Complete pivoting을 사용할 때에 다음을 만족함을 보였다.11
![]() ,
,
![]()
![]() 이라는 값은 컴퓨터를 통해 가우스 소거법으로 구한 값이다. 첫 번째 수식이 의미하는 것은,
이라는 값은 컴퓨터를 통해 가우스 소거법으로 구한 값이다. 첫 번째 수식이 의미하는 것은, ![]() 값을 수학의 세계에서 만족시키는 수학식은
값을 수학의 세계에서 만족시키는 수학식은 ![]() 에
에 ![]() 만큼의 오차를 적용하면 구할 수 있다는 것이다.
만큼의 오차를 적용하면 구할 수 있다는 것이다. ![]() 의 값은 두 번째 수식에 의해 범위가 정해진다. 이 값이 받아들일 만한 수준이면 우리는 컴퓨터로 계산한 결과를 마음 놓고 인정할 수 있게 된다. 윌킨슨이 전쟁 중에 계산했던 12개짜리 방정식은 이 기준에 비추어 보았을 때
의 값은 두 번째 수식에 의해 범위가 정해진다. 이 값이 받아들일 만한 수준이면 우리는 컴퓨터로 계산한 결과를 마음 놓고 인정할 수 있게 된다. 윌킨슨이 전쟁 중에 계산했던 12개짜리 방정식은 이 기준에 비추어 보았을 때 ![]() 값이 충분히 작았던 셈이다.
값이 충분히 작았던 셈이다.



답글 남기기