존 매카시

알골 언어

고급 프로그래밍 언어를 만들기 위한 노력으로 미국과 유럽의 컴퓨터 과학자들이 모여 만든 언어가 알골^Algol이다. 비록 알골 언어가 실제 현장에서 사용되는 언어로는 성공을 거두지 못했지만, 알골 언어에 포함된 많은 개념들은 후에 등장한 언어들에 많은 영향을 끼쳤다.

이미 앞에서도 설명한 바와 같이, 매카시는 알골 언어 설계에도 깊숙이 관여했다. 그는 미국 대표단 네 명 중 한 명이었으며 조건 분기와 재귀적 호출이 언어에 반영될 수 있도록 적극적으로 주장했다.

알골 60과 관련해서 저는 위원회에 속해 있었습니다. 위원회가 전반적으로 아주 야심이 대단했었고 그래서 나는 조건식^{conditional expression}과 불 연산식^{boolean expression}을 밀어 넣었습니다. 그런데 별로 마음에 들게 들어가지 않았어요.¹⁶

비단조 추론

비단조 추론^{non-monotonic reasoning}은 비단조 논리^{non-monotonic logic}를 사용한 추론이다. 비단조 논리를 이해하려면 먼저 단조 논리^{monotonic reasoning}가 무엇인지부터 알 필요가 있다.

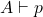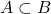어떤 논리가,  이고  이면 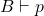 를 만족한다면, 그 논리는 단조적이다.¹³

위의 정의를 해석하면 이렇다. $A$ 란 어떤 사실^fact들이 모여 있는 집합이다. $A \vdash p$ 가 뜻하는 것은, $A$ 에 속하는 사실들이 참이라고 할 때, $p$ 라는 명제가 참이라는 것이다. 상식에 기반한 추론이라고 볼 수 있다. 내가 알고 있는 사실들( $A$ )로부터 어떤 것( $p$ )을 도출해낸 것이다. 그런데 $A$ 를 포함하는 $B$ 라는 집합이 등장한다. 이 집합은 $A$ 를 포함하므로 $A$ 에 뭔가 새로운 사실이 추가되었다는 의미이다. 내가 지금까지 알고 있던 상식(지식)에 새로운 사실이 추가되었다는 것이다. 그러면 여전히 $p$ 라는 명제는 사실일까? 만약 사실이라면 우리가 사용하는 이 추론은 단조 추론이다. 그런데 만약 그렇지 않다면? 즉 내가 모르던 사실을 알게 되자 그동안 참이라고 믿었던 것이 이제는 거짓이 되는 상황이 발생할 수도 있다는 이야기이다. 그렇다면 이 경우에 사용하는 이 추론은 비단조 추론이다.

수학에서 사용하는 논리는 단조적이다. 어떤 수학자가 뭔가를 증명했는데, 갑자기 새로운 사실을 알게 되어 그 증명이 무효화되는 일은 없다. 하지만 물리학에서는 그럴 수도 있다. 예를 들어 우리는 아주 오래전에 지구는 평평하다고 믿었다. 하지만 달에 비친 그림자를 보고 그렇지 않을 수도 있다는 생각을 가지게 되었고, 궁극적으로는 우주에서 지구를 바라본 순간 지구는 평평하다는 명제는 완전히 거짓이 되었다.

매카시는 1970년대에 비단조 추론에 관심을 가졌다. 상식에 기반한 추론이란 비단조적일 수밖에 없었기 때문이다. 완벽하게 수학적 논리로만 인간의 추론을 모델링하기에는 한계가 있었다.

인간이 하는 많은 추론이 단조적이기는 하지만, 상식에 기반한 일부 중요한 추론은 그렇지 않다. 우리는 어떤 주어진 가정들에 기반하여 결론에 도달하지만 만약 거기에 다른 가정이 추가되었다면 그런 결론에 도달하지 않았을 수 있다.¹³

매카시가 추구했던 인간 수준의 인공지능은 그의 예상보다 훨씬 어려웠다. 다트머스 인공지능 워크샵과 그 후 일련의 연구에서 얻었던 장밋빛 기대는 현실화되지 않았다. 오히려 지지부진한 상태가 계속되자 인공지능에 대한 회의론이 강하게 대두되기도 했다. 대표적인 것이 철학자 존 설^{John Searle}의 중국어방 이야기¹¹이다. 존 설은, 어떤 컴퓨터 프로그램이 지능을 가진 것처럼 보일 수는 있지만 그저 주어진 지시에 따라 움직이는 것이므로 지능을 가졌다고 말할 수 없다고 주장했다.

기호주의 AI를 통해서 인간 수준의 인공지능을 (아직까지는) 구현하지 못했을지 모르지만, 완전하게 실패했다고도 보기 어렵다. 이미 Logic Theorist에서 확인된 바와 같이, 적용 상황을 특정한 범주 내로 한정할 경우에는 논리와 규칙에 의한 추론이 가능성을 보여주었기 때문이다. 기호주의 AI는 전문가 시스템^{expert system}이라는 응용에서 상당한 성공을 거두었다.

계산복잡도

매카시가 간접적으로 큰 영향을 미친 연구 분야가 계산복잡도^{computation complexity}이다. 계산복잡도란, 어떤 문제가 컴퓨터로 풀기에 시간이 오래 걸릴지 아닐지를 판별하는 일종의 지표이다. 계산복잡도 분야는 마이클 래빈^{Michael Rabin}에 의해 시작되었는데 그 계기는 매카시와의 우연한 만남이었다.

1958년 여름에 마이클 래빈은 IBM에서 단기 인턴 일을 하고 있었다. 그런데 마침 매카시가 IBM에서 여름을 보내기 위해 그곳에 와 있었다. 왜 그랬는지는 알 수 없으나 아무튼 어느 날 매카시는 래빈에게 다음과 같은 문제를 냈다.

전쟁을 벌이고 있는 두 나라가 있다. 각각 A, B라고 하자. A라는 나라에서는 B라는 나라로 첩자를 보낼 계획이다. 이 첩자들은 국경을 넘어서 B라는 나라로 들어갔다가 다시 국경을 넘어 돌아와야 한다. 그런데 이들이 되돌아올 때 적군으로 오인을 받아서 아군에 의해 사살될 위험이 있다. 이를 피하려면 뭔가 암호를 사용해야만 한다. 예를 들어 “1932년 6월 20일”을 암호로 정하고, 첩자로 선발된 아군과 국경을 지키는 아군이 이를 숙지하면 된다.
하지만 아직도 문제가 있다. 국경을 지키는 아군들이 부주의하게 떠들다가 암호를 입 밖에 내고 이를 적군의 첩자가 엿들어버리면 암호가 무용지물이 되어 버린다. 자, 그렇다면 어떤 방법을 써야 할까?¹⁷

래빈은 이 문제에 대해 해법을 내놓았는데 이 과정에서 ‘계산하기 어렵다는 것’에 관해 고민하기 시작했고 결국 계산복잡도라는 분야를 개척했다.

^*
출처: https://en.wikipedia.org/wiki/John_McCarthy_(computer_scientist), CC BY-SA 2.0
^†
출처: https://history-computer.com/lisp-programming-language-guide/
^‡
아직 인공지능이라는 말이 만들어지기 전이었으나 편의상 이렇게 표현하겠다.
^§
출처: raysolomonoff.com
^¶
이것은 통상적인 프로그래밍 문법에 맞지는 않으나 편의상 이렇게 적었음에 유의하자.
^#
스택이라는 용어를 처음 사용한 이는 에드스거 다익스트라로 알려지고 있다.
^**
실제로는 두 가지 종류로 나뉜다. 일반 명령어는 operation code부 (18비트), adress 부 (15비트), tag부 (3비트)의 형태이다.
^††
이는 마치 자바스크립트에서 callback 함수를 인자로 사용하는 것과 유사하다.
^‡‡
그는 인공지능 연구소가 고용한 프로그래머 중 한 명이었다.
^§§
오늘날 신경망 AI가 성공적으로 사용되고는 있지만 설명할 수 없는 AI라는 지적을 받고 있다.
^¶¶
인터럽트란, 정상적인 흐름으로 동작하고 있는 프로세서를 잠시 다른 일을 하도록 강제로 만드는 하드웨어적인 기능이다.
^##
당시에는 시분할이 아니라 시간도둑(time-stealing)이라고 불렀다.
^***
1990년에 튜링상을 수상했다.
^†††
BBN은 후에 인터넷의 전신인 ARPANET용 시스템을 만든 회사이다.
^‡‡‡
출처: https://en.wikipedia.org/wiki/BBN_Time-Sharing_System, Public domain

참고문헌

1.
McCarthy J. Generality in artificial intelligence. ACM Turing Award Lectures. Published online 1986:1971. doi:10.1145/1283920.1283926
2.
ACM. JOHN MCCARTHY . A.M. Turing Award Laureate. Accessed July 26, 2022. https://amturing.acm.org/award_winners/mccarthy_1118322.cfm
3.
John McCarthy (computer scientist). Wikipedia. Accessed October 19, 2022. https://en.wikipedia.org/wiki/John_McCarthy_(computer_scientist)
4.
Oral History Interview with John McCarthy. Charles Babbage Institute; 1989:23. https://hdl.handle.net/11299/107476
5.
Nilsson NJ. John McCarthy 1927-2011: A Biographical Memoir. National Academy of Sciences; 2012:1-17.
6.
McCarthy J. Automata Studies. (Shannon CE, ed.). Princeton University Press; 1956.
7.
McCarthy J. History of LISP. SIGPLAN Not. Published online August 1978:217-223. doi:10.1145/960118.808387
8.
McCarthy J. Transcript of presentation. History of programming languages. Published online June 1978:185-191. doi:10.1145/800025.1198361
9.
McCarthy J. Programs with Common Sense. In: ; 1959.
10.
McCulloch WS, Pitts W. A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biophysics. Published online December 1943:115-133. doi:10.1007/bf02478259
11.
픽오버 클리퍼드 A. 인공지능: 100개의 징검이야기. 지식함지; 2020.
12.
마빈 민스키 -튜링상 수상자 시리즈. 지식함지. Accessed October 19, 2022. https://knowledgebasin.com/archives/persons/마빈-민스키
13.
McCarthy J. Artificial Intelligence, Logic and Formalizing Common Sense. Philosophical Logic and Artificial Intelligence. Published online 1989:161-190. doi:10.1007/978-94-009-2448-2_6
14.
McCarthy J. Memorandum to P. M. Morse Proposing Time-Sharing. Professor John McCarthy. Accessed July 26, 2022. http://jmc.stanford.edu/computing-science/timesharing-memo.html
15.
McCarthy J. Reminiscences on the History of Time-Sharing. IEEE Annals of the History of Computing. 1992;14(1):19-24.
16.
Guy Steele Interviews John McCarthy, Father of Lisp. InfoQ; 2009:1. https://www.infoq.com/interviews/Steele-Interviews-John-McCarthy/
17.
An Interview with Michael Rabin by David Harel. ACM; 2015:1.

컴퓨터 역사에 관한 콘텐츠를 제공합니다.

알골 언어

비단조 추론

계산복잡도

참고문헌

답글 남기기 응답 취소

공유하기

최근 출판물