공리적 의미론
프로그래밍 언어도 일반 언어와 같이 문법syntax과 의미semantics, 두 가지 특성을 가지고 있다. 문법에 어긋나는 말은 알아들을 수 없고 의미가 이상한 말은 의도를 파악할 수 없다. 프로그래밍 언어도 마찬가지이다.
알골 언어를 설계하는 과정에서 BNF 표기법이 등장하였고 이를 통해 문법을 공식적으로 표현할 수 있게 되었다.6 즉, 문법에 어긋나는 프로그래밍 코드를 체계적으로 알아낼 수 있게 되었다. 이에 비해 프로그래밍 코드의 의미를 체계적으로 표현하고 검증할 방법은 만들기가 쉽지 않았다. 그러던 중 1967년에 로버트 플로이드가 <프로그램에 의미 부여하기>7라는 논문을 발표하면서 돌파구가 마련되었다. 플로이드는 프로그램의 각 명령 단위command를 수식으로 표현한 후에, 프로그램의 수행 흐름을 따라가면서 수학적 추론을 통해서 이 수식을 전개했고, 최종적으로 도출되는 수식이 프로그램의 결과물을 표현하는 수식을 만족시킬 수 있는지를 보이려 했다. 프로그램의 각 명령 단위를 하나의 절대적 수식으로 표현했기 때문에 후에 ‘공리적 의미론axiomatic semantics‘이라고 불리게 된다.
토니가 프로그래밍 언어의 의미론에 본격적으로 관심을 쏟기 시작한 것은 회사 생활을 정리하고 국립컴퓨팅센터로 옮긴 후였다. 이 시기에 그는 비엔나에서 열린, 형식언어formal language에 관한 워크샵에서 수학 공리를 프로그래밍 언어에 적용해보자는 아이디어를 이미 제안했었고, 미발표 논문을 작성하기도 했다.5 그가 수학 공리에 관심을 가진 이유는 다음과 같다.
내가 대학으로 옮기려던 이유 중 하나는 … 프로그래밍 언어의 공리적 정의에 관심이 있었기 때문입니다… 나는 항상 수학에 관심이 많았고, 수학 분야의 주제는 관련 증명의 기초로 사용되는 공리에 의해 특징지어진다고 생각하고 있었습니다. 그래서 프로그래밍 언어의 의미를 정의하는 방법으로 공리를 사용하면 좋을 것 같다는 생각을 했죠. 그리고 공리에 끌렸던 (또 다른) 이유는, 그것이 다루고 있는 것에 대해서 완전한 묘사가 필요치 않다는 것이었습니다. 그저 증명에 유용한 정도면 충분했죠. 나는 프로그래밍 언어를 정의할 때 이런 특성을 원했습니다. 왜냐하면 당시에는 컴퓨터 제조사마다 자기 컴퓨터에 맞도록 프로그래밍 언어를 구현하고 있었기 때문이었습니다. 그래서 고급 언어들조차도 제조사의 하드웨어 사양에 따라 조금씩 달랐습니다.5
벨파스트의 퀸즈 대학교에 자리를 잡게 된 그는 이삿짐을 정리하다가, 조악하게 복사된 논문에 눈이 꽂히게 된다. 바로 로버트 플로이드의 논문이었다. 구해만 놓고 자세히 들여다보지 않았던 그 논문을 훑어본 그는, 자신이 추구하던 방법론과 일치함을 깨닫게 되었다. 임용 첫해의 바쁜 생활 속에서도 그는 시간을 내어 공리적 의미론을 보다 체계화하는 논문을 발표했다. <컴퓨터 프로그래밍을 위한 공리적 기반>8이라는 논문은 큰 반향을 일으켰다.
공리
공리axiom의 정의는 다음과 같다.
공리는 ‘참’이라고 받아들이는 문장statement이다. 추론이나 주장을 위한 전제 또는 시작점으로 사용된다.(위키피디아)9
그렇다면 토니는 이 공리를 어떻게 사용했을까? 그가 <컴퓨터 프로그래밍을 위한 공리적 기반>에서 열거한 공리 중 일부는 다음과 같다.
초등학교에서 산수 시간에 배우는 교환법칙, 결합법칙, 배분법칙 같은 것들이 공리인 셈이다. 6번이 조금 특이한데 그 이유는 컴퓨터의 하드웨어적 특징 때문이다. 뺄셈의 결과가 논리적으로 음수가 나올지라도 컴퓨터의 하드웨어에서는 그 결과값이 다르게 표현될 수 있으므로 그런 경우는 제외한 것으로 보인다. 6번에서 ![]() 은 일종의 조건문이다.
은 일종의 조건문이다. ![]() 의 왼편이 참일 경우, 오른편이 참이 된다는 의미로 해석한다.
의 왼편이 참일 경우, 오른편이 참이 된다는 의미로 해석한다.
위의 공리들은 컴퓨터에서 벌어지는 정수 연산에 대한 공리들이다. 이런 공리는 더 확장된다. 프로그래밍 언어에서 사용되는 대입문에 대해서도 공리를 정의할 수 있다.
호어 트리플
토니의 공리적 의미론에서 가장 눈에 띄는 것은 호어 트리플Hoare Triples이라는 표기법이다.
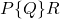
위의 표현은, “![]() 라는 프로그램 코드가 수행되기 전에
라는 프로그램 코드가 수행되기 전에 ![]() 가 참이면
가 참이면 ![]() 가 수행된 후에
가 수행된 후에 ![]() 은 참이다”라는 것을 의미한다. 만약
은 참이다”라는 것을 의미한다. 만약 ![]() 와는 상관없이
와는 상관없이 ![]() 가 수행된 후에
가 수행된 후에 ![]() 이 참이라면 사전 조건이 필요 없으므로 true
이 참이라면 사전 조건이 필요 없으므로 true![]() 과 같이 표현한다.
과 같이 표현한다.
호어 트리플이라는 표기법이 도입된 이유는, 대입문, 조건문, 반복문 등에 대한 공리를 표현하기 위해서이다. 대입문을 다음과 같이 표현한다면,
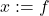
이 대입문에 대한 공리는 다음과 같이 호어 트리플로 표기할 수 있다.
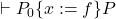
여기서 ![]() 는
는 ![]() 에 포함된
에 포함된 ![]() 를 모두
를 모두 ![]() 로 치환한 것을 의미한다. 이 호어 트리플을 해석하자면,
로 치환한 것을 의미한다. 이 호어 트리플을 해석하자면, ![]() 에 있는
에 있는 ![]() 를
를 ![]() 로 치환했을 때 참이라면
로 치환했을 때 참이라면 ![]() 라는 대입문이 실행된 후에
라는 대입문이 실행된 후에 ![]() 는 참이라는 의미이다. 이것은 공리이며 너무 당연하다.
는 참이라는 의미이다. 이것은 공리이며 너무 당연하다.
추론 규칙
공리들에서 새로운 추론을 만들어내기 위해서는 규칙이 필요하다. 토니는 몇 가지 추론 규칙들을 제시했는데 반복문의 경우는 아래와 같다.
while B do S 라는 반복문에 대해서 아래와 같은 규칙을 만들 수 있다.
만약 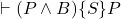 라면
라면 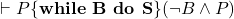 이다.
이다. 즉 P와 B가 참일 때 S를 실행한 후에도 P가 참을 유지한다면 위의 while 반복문을 실행한 후에는 P가 그대로 유지되고 B는 거짓이라는 값을 가진다는 의미이다. while 문이 끝났다는 것은 B가 거짓이 되었다는 것이므로 사실 당연한 이야기인데 단지 while 문이 끝난 후에 P가 계속 참인지를 확실하게 하기 위해 앞의 조건이 붙은 것이다.
추론 규칙은 이것 외에도 여러 가지가 있다.
적용 사례
프로그래밍 언어의 의미론이 목표로 하는 것은, 작성된 코드가 과연 주어진 문제에 대한 답을 정확하게 제공할 것인가이다.
앞에서 우리는 대입문이나 반복문을 어떻게 공리와 추론규칙으로 표현할지에 대해 보았다. 그런 공리와 추론규칙을 통해서 우리는 새로운 수식을 전개해나갈 수 있다.
만약 이 주어진 코드가 하려는 일, 즉 이 코드의 의도 또한 수식으로 표현하고, 앞의 공리와 추론규칙을 통해서 이 수식이 도출된다면 우리는 이 코드가 제대로 작성되었다고 말할 수 있을 것이다.
토니는 자신의 방법이 실제로 작동함을 보이기 위해 나눗셈을 예로 들었다. ![]() 를
를 ![]() 로 나누어서 몫에 해당하는
로 나누어서 몫에 해당하는 ![]() 와 나머지에 해당하는
와 나머지에 해당하는 ![]() 을 구하는 프로그램을 작성한다고 가정해보자. 아주 단순하게 작성하면
을 구하는 프로그램을 작성한다고 가정해보자. 아주 단순하게 작성하면 ![]() 에서
에서 ![]() 를 계속 빼면 된다. 언제까지? 나머지가
를 계속 빼면 된다. 언제까지? 나머지가 ![]() 보다 작아질 때까지이다. 이를 알골 60 스타일로 작성하면 다음과 같다.
보다 작아질 때까지이다. 이를 알골 60 스타일로 작성하면 다음과 같다.
r := x;
q := 0;
while (r >= y) do {
r := r - y;
q := q + 1;
}이 프로그램이 제대로 작성되었다고 했을 때 얻어지는 결과를 수식으로 표현하면 다음과 같다.
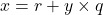
그렇다면 우리가 증명해야 할 것은 다음과 같이 표현된다.

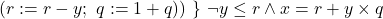
토니는 기본 공리들과 몇 가지 추론 규칙을 사용해서 위의 수식이 만족됨을 보였다.



답글 남기기