로버트 플로이드

튜링상 관련 업적

연산자 우선순위 파싱

어떤 문장이 주어졌을 때 그 문장을 단어 단위로 분해한 후 문법적 구조로 재구성하는 작업을 파싱^parsing이라고 한다. 파싱은 원래 언어학에서 사용하던 용어였고 이를 컴퓨터 과학에서 차용했다. 다음의 예를 보자.

나는 당신을 사랑합니다.

위의 문장을 파싱하면

주어(나는) - 목적어(당신을) - 술어(사랑합니다) - 마침표(.)

와 같이 문법적 규칙에 맞게 분해할 수 있다. 그런데 문장이 항상 이렇게 단순하지만은 않다.

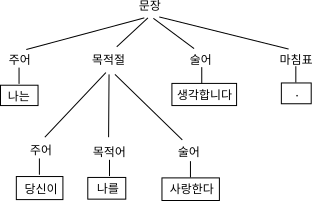
나는 당신이 나를 사랑한다고 생각합니다.

와 같은 문장을 파싱하면,

주어(나는) - 목적절(당신이 나를 사랑한다) - 술어(생각합니다) - 마침표(.)
       주어(당신이) - 목적어(나를) - 술어(사랑한다)

와 같이 계층적인 구조로 표현된다. 이런 계층적인 구조를 표현하기 위해 파싱 트리^{parsing tree}라는 방법이 사용된다.

컴퓨터 과학에서 파싱은 컴파일러 작업의 한 단계로 사용된다. 고급 프로그래밍 언어(예: C언어)로 작성한 프로그램을 문법에 맞게 분해하게 되면 미세한 단위로 동작을 나눌 수 있게 되며, 이 미세한 단위의 동작을 기계어 명령에 대응시킬 수 있다. 아래와 같은 단순한 사칙연산 프로그램 문장^statement을 생각해보자.

x = a + b * c;

위의 문장을 파싱하면 다음과 같은 파싱 트리가 생성되어야 한다.

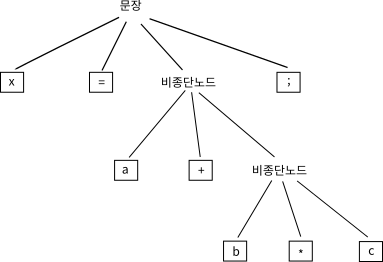
이 프로그램 코드가 정상적인 결과를 만들어내려면 파싱 트리의 최하단에서부터 작업을 진행해서 최상단으로 한 단계씩 거슬러 올라가면 된다. 파싱 트리의 각 노드는 하나의 기계어 명령어에 대응될 수 있다.^​§​

1950년대 후반에 알골^ALGOL이라는 고급 프로그래밍 언어가 제안되고 문법을 명확하게 정의할 방법인 BNF 형식이 도입되면서 많은 연구자들이 컴파일러 이론에 뛰어들었다. 파싱이란 결국, 어떤 프로그램 문장^statement이 주어졌을 때 이 문장의 구조를 표현할 수 있는 문법 명세^{syntax specifications}를 찾아내는 것이다. 예를 들어, 우리가 사용하려는 프로그래밍 언어가 다음과 같은 문법으로 정의되었다고 가정해보자.

S ::= V = A ;
A ::= A + B
A ::= B
B ::= B * C
B ::= C
C ::= (A)
C ::= V
V ::= a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z

그러면 컴파일러의 일부분인 파서^parser(파싱 작업을 하는 프로그램을 칭한다)가 해야 할 일은, x = a + b * c; 와 같은 프로그램 문장이 위의 문법 명세 중 어느 것들에 의해 표현이 되는지를 찾아내는 것이고, 그렇게 하다 보면 자연스럽게 앞의 그림과 같은 파싱 트리가 도출된다.

초창기 연구자들은 하향식^top-down 방식으로 문법 명세를 찾아냈다. 최상위 단계의 문법 명세부터 따져보면서 점차 세부적인 아래 단계의 문법 명세로 훑어나가는 식이다. 위의 예에서 생각해보자. 총 8개의 문법 명세 중에서 최상위 단계에 해당하는 것은 S ::= V = A ; 이다. 그래서 x = a + b * c; 라는 프로그램 문장이 주어지면 제일 먼저 여기에 맞춰본다. 이게 맞아떨어지려면 x가 V에 해당하고 a + b * c는 A에 해당하면 된다. 일단 이게 정답이라고 가정하고 이제 A에 관한 문법 명세를 찾아본다. 위의 문법에서는 두 개가 있다. 둘 중 하나를 선택해서 일단 진행한다. 여기서는 A ::= A + B를 선택했다고 가정하자. 그러면 a + b * c를 A + B에 맞춰본다. 이게 맞아떨어지려면 a는 A에 해당하고 b * c는 B에 해당해야 한다. 일단 이게 정답이라고 가정하고 계속 진행한다. 이제 해야 할 작업이 두 개로 늘어났다.

먼저 a부터 따져보자. a가 A에 해당한다고 했으므로 다시 A에 관한 문법 명세를 찾아본다. 일관성을 위해 아까처럼 A ::= A + B를 선택한다. a를 A + B에 맞춰보면 답이 없다. 왜냐하면 +라는 연산자가 나타나지 않기 때문이다. 그래서 A에 관한 두 번째 명세인 A ::= B를 사용해본다. 그러면 a는 B에 해당한다. 이제 B에 관한 문법 명세를 찾아볼 시간이다. B도 역시 두 개의 명세를 가지고 있다. 앞에서 했던 식으로 진행하면 B ::= C라는 명세가 적합하다. 이제 a는 C에 해당한다. C에 대한 명세도 두 개가 있고 C ::= V라는 명세가 적합하다. 이제 a는 V에 해당한다. V에 대한 명세는 한 개만 존재한다. 그리고 V는 알파벳 문자 중 하나임을 의미한다. 따라서 더 이상 진행할 필요가 없다.

아직 해야 할 일이 남아 있다. b * c의 문법 명세를 아직 끝내지 않았다. b * c는 B에 해당한다고 했으므로 B에 관한 문법 명세를 따져보자. B ::= B * C라는 명세가 맞아떨어진다. 이제 b는 B에 해당하고 c는 C에 해당한다. 앞에서 했던 식으로 진행하면 결국 V 문법 명세에 도달하게 되고 알파벳 문자이므로 더 이상 진행할 필요가 없다.

하향식 파싱은 직관적으로는 이해하기가 쉽지만 단점이 있다. 여러 개의 문법 명세가 적용 가능한 상황이 발생하면 일단 임의로 하나를 선택해서 진행하게 되는데, 그러다가 중간에 아니다 싶으면 뒤로 되돌아와서 다른 것으로 재시도를 해야 한다는 것이다. 이를 백트래킹^backtracking이라고 부르는데 프로그래밍 언어의 문법 구조가 복잡해지면 아주 비효율적인 상황이 발생한다.

플로이드는 이런 문제를 해결하는 방안으로 연산자-우선순위 파싱이라는 이름의 방법을 제안했다. 핵심적인 개념은 말 그대로 연산자들 사이의 우선순위를 미리 결정해 놓고 이를 이용하자는 것이다.^​¶​

실제 이 알고리듬이 동작하는 방식은 shift-reduce 방식이다. 한국어로 묘사하자면, “통과시키다가 때가 되면 정리”하는 방식이다. 위에서 예를 들었던 x = a + b * c ; 라는 프로그램 문장으로 설명하자면, x, =, a, +, b, *, c, ; 의 순서로 하나씩 통과시키다가 어떤 조건이 만족되면 필요한 만큼 정리하자는 것이다. 그렇다면 여기서 ‘어떤 조건’이란 무엇을 말하는가? 그것은 연산자 사이의 ‘우선순위’ 관계이다. 두 개의 연산자가 연달아 있을 때 둘 사이의 관계이다.

앞의 문법에 나타난 입력 토큰 사이의 우선순위는 다음과 같은 표로 나타낼 수 있다.

위의 표를 해석하는 방법은 다음과 같다. i번째 행, j 번째 열에 있는 우선순위 값은, i번째 열의 연산자 바로 뒤에 j 번째 행의 연산자가 나타날 경우 둘 사이의 관계이다. >라는 값은 앞에 오는 연산자의 더 우선순위가 높다는 것이고 <라는 값은 뒤에 오는 연산자가 더 우선순위가 높다는 것이다. 따라서 만약 * 다음에 +가 오면 *의 우선순위가 높다는 것이고 = 다음에 +가 오면 +의 우선순위가 더 높다는 것이다. 우선순위가 높은 것이 먼저 처리되어야 한다.

파서에 입력되는 프로그램 문장은 이미 문법적 단위로 분해된 상태임에 유의하자. 컴파일러에서는 파싱 단계를 진행하기 전에 낱말 분석^{lexical analysis}을 통해 프로그램 문장을 토큰^token 단위로 만들어 놓는다. 파서는 입력되는 토큰을 차례로 스택에 저장한다.^​ 새로 입력되는 연산자가 스택의 최상단에 저장된 연산자보다 우선순위가 높으면 계속 통과^shift시킨다. 새로 입력되는 연산자가 스택의 최상단에 저장된 연산자보다 우선순위가 낮으면 정리^reduce한다.

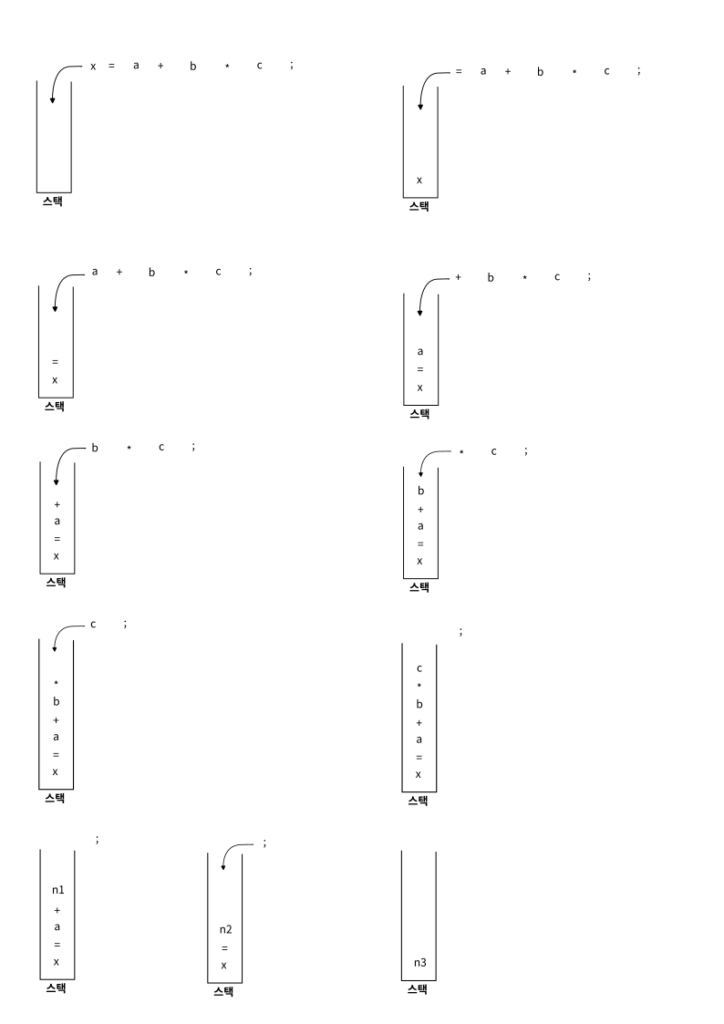
x = a + b * c ; 라는 문장이 처리되는 과정은 다음과 같다. 앞에서 언급했듯이 이 문장은 x, =, a, +, b, *, c, ; 의 순서로 파서에 의해 처리된다. =가 입력되면 이전에 입력된 연산자가 없으므로 그대로 스택^stack에 저장한다. +가 입력되면 스택의 맨 위에 있는 =와 우선순위를 따지는데 +의 우선순위가 높으므로 그냥 스택에 저장하고 계속 진행한다. 이제 *가 입력되면 스택의 맨 위에 있는 +와 비교한다. *가 +보다 우선순위가 높으므로 그냥 스택에 저장하고 계속 진행한다. 마지막으로 ;가 입력되면 스택의 맨 위에 있는 *와 비교한다. ;의 우선순위가 낮으므로 이제 정리^reduce가 이루어진다. *와 그 앞뒤에 있던 b, c가 하나로 묶이는데 b, *, c가 스택에서 사라지고 이를 대체하는 n1이라는 값이 스택에 저장된다. 이제 스택에는 x, =, a, +, n1이 들어 있다. ;는 다시 스택의 최상단에 있는 연산자 +와 비교된다. ;의 우선순위가 낮으므로 다시 정리^reduce가 진행된다. a, +, n1이 하나로 묶이면서 스택에는 이를 대체하는 n2라는 값이 저장된다. 이제 스택에는 x, =, n2가 들어 있다. 다시 ;는 스택의 최상단에 있는 연산자인 =와 비교가 이루어진다. 둘의 우선순위는 같다. 스택에 들어 있는 연산자의 우선순위가 같을 때는 스택에서 그다음으로 상단에 있는 연산자를 찾아서 비교해야 하는데 더 이상 연산자가 남아 있지 않다. 따라서 이 전체가 정리^reduce된다. x, =, n2, ; 가 하나로 묶이게 된다. 결국 이렇게 되면 파싱의 최종 결과는 다음과 같다.

n1 : b * c
n2 : a + n1
n3 : x = n2 ;

위의 결과를 그래프로 그리면 앞에서 보았던 파싱 트리와 동일하다. 그리고 이 파싱 결과물을 보면 이제 쉽게 기계어 코드로 변환할 수 있음을 알 수 있다.

연산자의 우선순위가 어떻게 사용되는지는 설명했으나 연산자 우선순위를 어떻게 알아낼지에 대해서는 아직 언급하지 않았다. 플로이드는 문법 명세 속에서 자동으로 연산자 우선순위를 뽑아내는 방법도 함께 알아냈다. 따라서 어떤 프로그래밍 언어에 대해서 문법 명세가 주어진다면 자동으로 연산자 우선순위를 알아낸 후, 앞에서 설명한 알고리듬을 사용하여 파싱을 할 수 있다.

플로이드의 방법은 파싱 트리를 가장 아랫단에서부터 시작하여 만들어가기 때문에 상향식^bottom-up 방식으로 불리며 백트래킹이 없기 때문에 하향식 방식에 비해 훨씬 효율적이다. 플로이드의 연구는 파싱 연구에 새로운 전기를 마련했으며 현재도 계산기와 같은 산술연산용 컴퓨터에 널리 사용되고 있다. 하지만 단점이 있다. 그의 방법은 비연산자^non-terminal가 연달아 나오는 문법에는 적용하기가 어렵다.

또한, 같은 개념의 파싱이 1963년에 에드스거 다익스트라에 의해서도 발표되었는데 작성한 시기는 플로이드보다 앞서는 것으로 여겨진다.^​13​

1 2 3 4 5