프로그래밍 언어 의미론

언어에는 문법syntax과 의미semantics가 있다. 문법에 맞지 않는 말은 도대체 무슨 소리인지 어리둥절하게 된다. 문법에는 맞지만 의미가 이상한 말도 있다. 이런 말을 들으면 정신 나간 소리로 느껴진다. 후자의 경우로 대표적인 예문을 들자면, ‘무색의 초록색 아이디어가 맹렬히 잠잔다​14​‘가 있다. ‘초록색이 무색’이라고 하는 것도 이상하고 ‘아이디어가 잠을 잔다’는 것도 말이 안 되며 ‘맹렬히 잠잔다’는 표현도 어색하다.

프로그래밍 언어에서도 문법과 의미를 따진다. 문법은 고급 프로그래밍 언어로 작성한 코드를 기계어로 변환하기 위해 필요하다. 약속된 규칙을 준수해야만 제대로 변환이 가능하다. 프로그래밍 언어에서 의미semantics는 프로그램 코드의 의도를 의미한다. 예를 들어 산술 평균을 계산하는 코드를 수행했을 때 기하 평균값이 나온다면 ‘의미’적으로 오류가 있는 것이다.

프로그래밍 언어의 문법은 BNF 형식이 나오면서 체계가 잡혔다. 컴파일러는 낱말 분석, 파싱 등의 과정을 진행하면서 프로그래밍 코드에 있을 수 있는 문법적 오류를 찾아낸다.​#​

컴퓨터 과학자들은 프로그램의 ‘의미’도 ‘문법’처럼 어떤 약속된 규칙과 절차에 의해서 오류를 찾아내고 싶었다. 하지만 쉽게 방법을 찾아내지 못했다. 그래서 결국 프로그램이 제대로 동작하는지 검증하기 위해서는 실제로 프로그램을 실행시켜보는 수밖에 없었다.

사람들은 코드를 작성한 후에 테스트용 실행을 한다. 그러면 버그가 발견되고 수정을 한다. 그러다가 점점 더 버그를 발견하게 되고 계속 더 수정을 하는데 더 이상 오류를 찾을 수 없게 되면 끝이 난다. 하지만 언제 내일이라도 새로운 버그가 튀어나와서 새로운 형태의 문제를 일으킬지 모른다는 두려움에 사로잡혀 산다.​2​

플로이드는 프로그램이 의도대로 동작함을 증명하는 방법을 찾고 싶었다. 1967년에 그는 <프로그램에 의미 부여하기​10​>라는 논문을 발표해서, 프로그램의 각 명령 단위command를 수식으로 표현한 후 수학적 추론을 통해 프로그램의 수행에 오류가 있는지를 알아내는 방법을 제안했다.​10​ 이 방식은 명령 단위의 의미를 수학적 수식axiom으로 표현하는 특징을 가지고 있어서 공리적 의미론axiomatic semantics이라고 부른다.

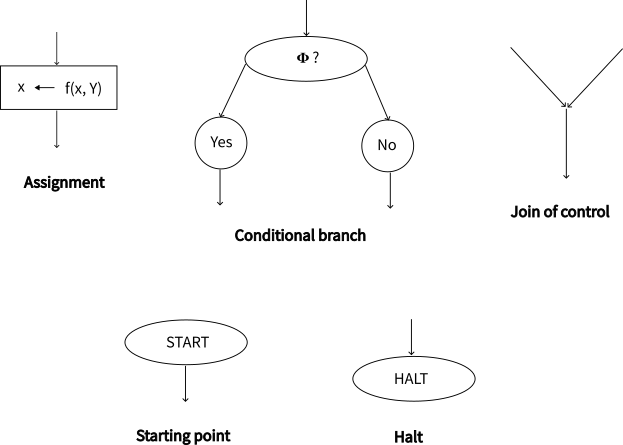
플로이드의 방법에서 핵심 중 하나는 어떤 유형의 명령 단위command마다 의미 정의semantic definition를 하는 것이다. 플로이드는 순서도flowchart를 기반으로 명령 단위의 유형을 나누었는데, 대입assignment, 조건 분기conditional branch, 제어 합류join of control, 시작starting point, 종료halt 등이 있다.

순서도에 사용되는 명령 단위들​10​

그렇다면 의미 정의란 무엇일까? 각 유형의 명령 단위마다 수행 직전의 상황과 수행 직후의 상황을 수학적으로 표현하는 것이다. 대입을 예로 들어보자. 대입은 x \gets f(x, Y)라고 모델링할 수 있다. 여기서 Y는 x가 아닌 다른 변수들을 의미한다. 그리고 대입이 수행되기 직전의 상황이 P(x, Y)라는 수식에 의해 표현된다고 하자. 즉, 변수 x를 포함하여 여러 변수가 포함될 수 있는 어떤 수식이다. 그렇다면 대입이 수행되면 (\exists x_0)(x = f(x_0, y) \land P(x_0, y)가 만족된다. 이 결과값에서 추론될 수 있는 수식들 즉, (\exists x_0)(x = f(x_0, y) \land P(x_0, y) \vdash Q_1 이라고 할 때 Q_1 들은 모두 참이다.

조건 분기는 의미 정의는 어떻게 될까? 조건 분기는 조건식의 값에 따라 서로 다른 두 개의 결과를 가져온다. 조건식 직전의 상황이 P이고 조건식의 값이 \Phi 라고 한다면 조건식을 수행한 후에는 P \land \Phi 와 P \land \neg\Phi 라는 두 가지 상황이 가능해진다. 따라서 이 두 가지 결과에서 추론되는 수식들, 즉 P \land \Phi \vdash Q_1이라 하고 P \land \neg\Phi \vdash Q_2 라고 할 때 Q_1과 Q_2는 모두 참이 된다.

제어 합류의 의미 정의는 P_1 \lor P_2 \vdash Q_1 이다. 여기서 P_1과 P_2는 합류되는 두 입력 간선 각각의 상황을 수식으로 표현한 것이다. P_1에서 추론되거나 P_2에서 추론되는 것은 모두 참으로 본다는 의미이다.

명령 단위의 유형마다 이렇게 의미 정의를 하게 되면, 실제 순서도에 적용할 수 있다. 순서도 상에 나타나는 각 명령 단위마다 해당되는 의미 정의를 적용하면 그 명령 단위가 수행된 후의 상황이 수식으로 표현된다.

그렇다면 이것을 이용해서 프로그램의 정확성을 어떻게 검증할 수 있을까? 두 가지 방법이 있다. 첫 번째 방법은 프로그래머가 일단 순서도 상에 나타나는 각 명령 단위마다 자신이 의도한 결과를 수식으로 표현한 후에, 그 수식이 의미 정의에 의해 추론 가능한지를 확인하는 것이다. 두 번째 방법은 의미 정의를 이용해서 프로그램의 최종 결과값을 유도한다. 순서도에서는 각 명령 단위가 간선으로 연결되어 있다. 따라서 어떤 명령 단위에 의미 정의를 적용하여 그 결과값을 수식으로 추론해내면, 바로 다음에 이어지는 명령 단위의 입력 조건으로 사용할 수 있다. 순서도에서 프로그램의 수행 흐름을 따라 이를 계속 진행하면 마지막 단계에서 프로그램의 최종 상황을 수식으로 얻을 수 있다. 이 결과값이 프로그램의 의도에 부합하는지를 확인하면 된다.

플로이드는 자신의 방법을 알골 언어에도 적용했다. 이를 위해 if then else 문, for 문, 복합문에 대한 의미 정의가 추가되었다. 따라서 이론적으로는 알골 언어로 작성한 프로그램에 대해 수학적으로 프로그램의 정확성을 증명할 수 있다.

하지만 플로이드의 방법은 몇 가지 한계를 지녔다. 먼저, 대입문의 경우 부수 효과side effect가 있는 경우에는 사용할 수 없다. 앞에서 대입문을 x \gets f(x, Y) 라고 정의하고 Y는 변수 x가 아닌 다른 변수들을 의미한다고 설명했다. 그런데 Y에 있는 변수 중에 어떤 것이 변수 x에 종속되어 있다면 플로이드의 방법은 사용할 수 없다. 또한, 복합문의 경우에 내부 변수가 외부의 변수와 같은 이름을 사용하면 플로이드의 방법을 바로 적용할 수 없다. 왜냐하면 수식에서 같은 이름으로 서로 다른 변수를 표현할 수 없기 때문이다. 이런 경우에는 복합문 내부에 있는 변수의 이름을 다르게 바꿔준 후에 적용해야 한다.

이렇듯 실제 적용하기에는 몇 가지 제약이 있고, 수식을 도출하고 전개하는 과정이 쉽지 않다는 단점을 가지고 있기는 하지만, 컴퓨터 프로그램의 의미를 수식으로 형식화하고 이를 통해 정확성을 검증하는 길을 최초로 열었다는 점에 플로이드의 방법은 큰 의미를 지닌다. 그의 방법은 토니 호어​#​에 의해 더 발전되었고 공리적 의미론이라는 하나의 흐름이 되었다.

1 2 3 4 5