마빈 민스키

튜링상 관련 업적

마빈 민스키가 인공지능 분야에서 차지하는 자리는 그 누구보다도 크다고 할 수 있다. 튜링상 선정 이유에서도 볼 수 있듯이 그는 인공지능이라는 분야를 세운 사람이다.

하지만 1969년을 기준으로 생각한다면 조금 의아할 수도 있다. 당시 그의 나이는 42세였다. 그 이전의 수상자들과 비교하면 상당히 젊은 나이였다. 또한, 그가 MIT의 인공지능 연구소를 만들어서 인공지능 연구의 선두에 있었던 것은 맞지만 한 획을 그었다고 할 만한 결과물을 꼭 집어내기가 쉽지 않다. 오히려 당시에 인공지능 연구의 또 다른 선두 그룹이었던 카네기 멜런 대학교의 앨런 뉴얼^{Allen Newell}팀은 Logic Theory Machine, General Problem Solver 등의 눈에 띄는 결과물을 만들어 놓은 상태였고, 함께 활동했던 존 매카시는 이미 리스프^LISP 언어라는 걸출한 결과물을 가지고 있었다. 후에 존 매카시와 앨런 뉴얼도 튜링상 수상자로 선정되기는 했으므로 결국 받을 사람은 다 받았다고 할 수 있겠으나, 순수하게 연구 결과물만 놓고 보자면 마빈 민스키가 그들보다 먼저 튜링상을 받게 된 점은 납득하기 어려운 구석이 있다.

하지만 선정 이유에 나와 있듯이 그가 인공지능 분야를 세우고, 틀을 잡고, 널리 알리는 데 큰 역할을 한 것은 부인하기 어렵다. 아직 전자식 컴퓨터가, 빠른 숫자 계산기 정도로 인식되던 시절에 그는 지능을 가지는 기계에 대한 비전을 제시했다. 그가 지도한 학생들은 미국의 다른 대학교들로 퍼져서 인공지능 연구를 이끌었고 산업계에서 두각을 나타내는 이도 있었다. 또한 그도 인정했듯이 초창기에는 인공지능과 직접적인 연관성은 없더라도 새로운 도전들이 인공지능이라는 이름 아래에서 이루어졌다. 따라서 그는 뛰어난 인재들을 끌어모으고 새로운 시대를 잉태시킨 선구자이자 선지자로서 높이 평가받았다고 보아야 할 듯싶다.

그가 튜링상으로 선정된 1969년까지 했던 주요 작업들을 살펴보겠다.

신경망 이론

신경망 이론은 마빈 민스키를 인공지능의 세계로 안내한 장본인이다. 앞에서 서술한 바와 같이 마빈 민스키가 인공지능의 세계에 발을 디디게 된 계기는 하버드 대학교 학부생 시절로 거슬러 올라간다. 와이드너 도서관에서 <수학적 생물리학^{Mathematical Biophysics}>이라는 책에 소개되어 있던 매컬럭-피츠의 신경망 이론을 접하고 인공지능에 관심을 가지게 되었다고 그는 회고했다.^​2​

그의 관심은 박사과정 시절에 다시 살아났다. 그는 실제로 매컬럭을 만나서 의견을 나누었고 신경망을 구현하여 간단한 강화 학습 시스템을 만들기도 했다. 그가 1951년에 만든 SNARC(Stochastic Neural Analog Reinforcement Calculator)는 이름이 의미하는 바와 같이 신경망 이론을 적용하여 만든 아날로그 방식의 확률식 강화 학습 시스템이다.

SNARC는 40개의 뉴런^neuron으로 구성되었는데 각 뉴런은 맥컬럭-피츠 이론에 나오는 뉴런과 흡사했다. 뉴런에는 입력 단자와 출력 단자가 있는데 입력 단자로 들어오는 신호를 출력 단자로 전달할지 여부는 어떤 확률값에 의해 결정되었다. 이 확률값이 0 또는 1이 아니라 0에서 1 사이의 값이라는 점에서 매컬럭-피츠의 뉴런과 차이가 있다.^​#​ 이 확률값은 분압기^{potentiometer}를 써서 구현되었는데 분압기에는 볼륨 조정용 다이얼처럼 생긴 단자가 붙어 있었다.

마빈 민스키는 물리학과 대학원생인 딘 에드먼즈^{Dean Edmonds}의 협력을 받아 SNARC를 완성했고 이를 사용해서 미로 찾기를 학습시켰다고 한다. 안타깝게도 SNARC는 현재 실물이 온전하게 남아 있지 않고 한 개의 뉴런에 해당하는 구성품만 남아 있다.

SNARC 뉴런은 몇 개의 진공관과 커패시터, 분압기, 전구, 클러치 등으로 구성되었다. 분압기는 입력 단자에서 출력 단자로 신호가 전달될 확률값을 결정하는데 볼륨 조절 다이얼 같은 방식으로 조절되었다. 궁극적으로 SNARC에서 뉴런이 학습을 통해 결정하게 되는 것이 이 분압기의 값이다.

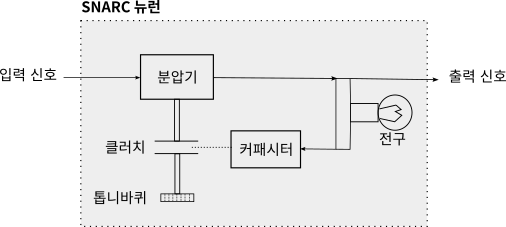
학습의 이루어지는 방식은 다음과 같다. 뉴런의 출력 단자에는 커패시터^capacitor가 달려 있어서 입력 단자의 신호가 출력 단자로 넘어오면 이 커패시터가 충전된다. 커패시터에는 ‘클러치’가 붙어 있는데 커패시터에 충전된 전압이 일정 수준을 넘으면 ‘클러치’가 닫힌다. 클러치가 닫히면 원형 톱니바퀴와 분압기 조절 단자가 연결된다.

원형 톱니바퀴에는 일종의 자전거 체인 같은 것이 걸려 있다. 실험자는 뉴런에게 학습을 명령하기 위해 어떤 버튼을 누른다. 버튼을 누르면 모터가 작동하면서 이 자전거 체인이 조금 움직인다. 체인이 움직이면 톱니바퀴가 살짝 돌아가게 된다. 만약 클러치가 닫혀 있다면 분압기 조절 단자가 함께 회전하게 되어 분압기의 값을 조정하는 효과를 가져온다. 커패시터는 시간이 지나면 방전되는 특징을 가지고 있다. 따라서 시간이 흘러 커패시터가 방전되면 클러치는 떨어진다.

민스키의 인공지능 기계 SNARC에는 총 40개의 뉴런이 사용되었다고 한다. 이 40개의 뉴런에 있는 톱니바퀴들은 모두 자전체 체인에 물려 있었다. 그래서 학습을 명령하는 버튼을 누르게 되면 이 40개의 톱니바퀴들이 모두 살짝 돌아가게 되는데, 그중에서 클러치가 닫혀 있는 뉴런에서만 분압기의 값이 변경된다.

SNARC에서 강화 학습이란 결국 40개의 뉴런에 있는 분압기의 값, 즉 입력 신호를 출력 단자로 전달할 확률값 40개에 대해서 최적의 값을 구하는 것이었다. 그렇다면 SNARC에서 말하는 ‘최적’이란 무엇을 위한 최적인가? 안타깝게도 정확하게 어떤 실험을 했는지에 대한 온전한 자료가 남아 있지 않다.^​††​ 단지 민스키의 인터뷰를 통해서 추측만 할 수 있는데, 그는 “쥐”의 미로찾기 실험에 비유했다. 그의 단편적인 설명에서 유추해본 SNARC의 전체적인 동작 방식은 다음과 같다.

하나의 입력 단자와 하나의 출력 단자를 가지는 뉴런 40개를 무작위로 연결한다. 어떤 출력 단자는 복수 개의 입력 단자들에 연결될 수도 있고, 어떤 출력 단자는 연결이 되지 않을 수도 있을 것이다. 그리고는 같은 뉴런에 속하지 않는 입력 단자 한 개와 출력 단자 한 개를 선정한다. 이제 이 입력 단자에 전기 신호를 가하면, 선정된 출력 단자까지 신호를 전달하는 최적의 경로를 찾아내야 한다. 선정된 입력 단자를 미로의 입구, 선정된 출력 단자를 미로의 출구라고 생각하면 이것은 “쥐”의 미로찾기 실험과 유사해진다.

자. 이제 선정된 입력 단자의 뉴런에서는 분압기에 의해 설정된 확률값에 따라 이 신호가 출력 단자로 전달될지가 결정될 것이다. 만약 출력 단자로 신호가 전달된다면 이 출력 단자가 연결된 다른 뉴런 혹은 뉴런들에서 역시 같은 식으로 신호의 전파가 결정된다. 뉴런 사이의 연결은 무작위로^random 이루어져 있으므로 어느 뉴런으로 신호가 전달될지는 예견할 수 없다. 한 가지 확실한 것은 신호가 분압기를 통과한 뉴런에서는 전구에 불이 들어온다는 것이다. 실험자는 어느 뉴런에 불이 들어오는지를 보고 원하는 방향으로 신호가 전달되고 있는지를 알 수 있다. 만약, 신호의 전달 경로가 마음에 든다면 학습을 시키기 위해 자전거 체인을 구동시키는 버튼을 누른다. 그러면 불이 들어온 뉴런들의 분압기 값, 즉 확률값이 증가한다. 해당 뉴런은 신호를 전파할 확률이 증가하는 셈이다. 이제 다시 기계의 전원을 껐다가 다시 켠다. 뉴런의 전구에 불이 들어오는 것을 보고 마음에 들면 버튼을 누르고, 마음에 들지 않으면 전원을 껐다가 다시 켠다.

이런 과정을 계속 반복한다고 해서, 과연 선정된 출력 단자까지 신호가 전달될지는 민스키도 확신하지 못했다. 그런데 놀랍게도 선정된 출력 단자에 있는 전구에 불이 들어왔다. “쥐”가 길을 찾아서 출구로 빠져나간 것이다. 한 가지 확실치 않은 점은, 민스키가 시작 입력 단자를 지정했는가이다. 그는 인터뷰에서 아래와 같이 회상했다. 여기서 “쥐”란 불이 들어온 전구를 의미한다.

우리가 했던 설계가 가지고 있는 전기적 우연성 때문에 그 미로 안에 한꺼번에 두 마리 혹은 세 마리의 쥐가 나타나기도 했습니다. 그 쥐들은 사실 서로 상호작용을 했습니다. 하나가 좋은 경로를 찾으면 다른 녀석들이 그 경로를 따랐지요. 그 기계를 바라보면서 우리는 한참 동안 과학에 대해 잊었습니다. 그렇게 작은 신경 시스템에서 한 번에 여러 개의 활동이 진행될 수 있다는 것이 놀라웠습니다. 그리고 연결을 무작위로 했기 때문에 일종의 안전장치 효과가 있었습니다. 뉴런 중 하나가 고장 나더라도 전체적으로는 문제가 없었죠.^​4​

사실 굳이 첫 시작 입력 단자에서부터 불이 들어올 필요는 없을 것이다. 어찌 되었건 결국에 가서는 시작 단자에서 출발하는 경로를 알아낼 수 있기 때문이다.

SNARC는 최초로 구현된 신경망 학습 기계로 여겨진다. 그런데 반전이 있다. 박사 학위 논문 제목이 <아날로그 신경망 강화학습 시스템 이론과 뇌 모형 문제에 대한 적용>^​10​일 정도로 신경망에 애정을 가졌던 그는 후에 입장을 완전히 바꾸게 된다. 그 이유는 아래의 인터뷰에서 엿볼 수 있다.

사실 나는 기호^symbol 방식의 접근을 시작하기 전에 최초의 신경망 학습 기계를 만든 적이 있습니다. 그 기계는 나를 화나게 만들었는데 왜냐하면 처음에는 아주 빠르게 학습했지만 갈수록 느려졌기 때문이었습니다. 그리고 새롭게 다른 방향으로 학습해보려면 예전 것은 모두 버려야 했죠. 그래서 어려운 학습을 하기에는 구성이 충분치 않다고 생각했습니다… 요즘 여기저기에서 신경망을 이용해 이런 것을 해보았네, 저런 것을 해보았네 하는 발표들이 나옵니다만 그저 하나의 사례에 불과합니다. 신경망이 어떤 문제를 풀었다면 내 느낌으로는 그 문제가 사람들이 생각하는 것보다는 쉬웠기 때문이었던 것 같은데 나의 이런 견해에 화가 난 사람들이 많습니다. 하지만 화를 낼 것이 아니라 그 문제가 기술적인 면에서 어려운 것임을 보여주는 이론을 정립해야만 할 것입니다.^​11​

1958년에 퍼셉트론이라는 신경망 회로를 발표한 로젠블랫과 그의 논쟁은 유명하다. 후에 그는 이렇게 회상했다.

로젠블랫은 아주 강력한 주장을 들고 나왔는데 도저히 처음에는 믿을 수가 없었습니다…. 로젠블랫의 추측은 결국 수학적으로 옳음이 증명되었습니다. 굉장히 어려운 증명이었고 그래서 나는 로젠블랫이 그것을 추측한 것에 대해 지금도 큰 존경심을 가지고 있습니다. 하지만 내가 당시 우려했던 것은 그가 주장하는 기계가 할 수 없는 것들이었습니다. 예를 들어 그의 기계는 ‘E’와 ‘F’를 구별하고, ‘5’와 ‘6’을 구별합니다. 하지만 그 글자 주변에 아무 연관없는 것들이 방해물로 있으면 제대로 인식하지 못합니다. 퍼셉트론 지지자들은 아주 명확한 예를 사용하고 있어서 실험적으로 오도되고 있다고 나는 생각했습니다… 자, 여기 그릇 뒤에 숟가락이 있다고 해봅시다. 숟가락의 손잡이 부분과 반대편 맨 끝부분만 눈에 보여도 우리는 그것이 숟가락임을 알아챕니다. 하지만 퍼셉트론은 알아채지 못합니다. 사람도 사실 마찬가지입니다. 다른 알고리듬을 추가로 사용하지 않으면 알 수 없습니다.^​4​

1 2 3 4 5 6