기타 업적

π-calculus

π-calculus는 동시성을 수학적으로 표현하는 방법 중 하나이다. CCS에서 발전된 것으로 이름붙이기naming에서 변화가 있었다. CCS에서는 기본적으로 기계machine들 사이의 상호 작용이라는 관점에서 접근했다. 하지만 π-calculus에서는 이름이 붙는 것들을 모두 프로세스process라고 간주한다. 여기서 말하는 프로세스는 상호작용에 참여하는 능동적인 개체active entity이다. 이렇게 되면 메모리 상의 변수도 하나의 프로세스가 된다.

예를 들어 두 개의 프로그램이 하나의 공유 변수를 통해서 통신하고 있다고 가정해 보자. π-calculus에서는 이 두 개의 프로그램뿐만 아니라 메모리 상에 있는 공유 변수도 하나의 능동적인 프로세스라고 본다.

π-calculus라는 이름은 λ-calculus를 염두에 두고 지은 것이다.

“pi”는 프로세스를 뜻하기도 하고 포인터를 의미하기도 하며 병렬처리 기타 등등을 말하기도 합니다. 중요한 점은 진짜 이유는 없다는 겁니다. 그냥 그게 발음하기 아주 쉽다는 생각이 들었습니다. 그리고 실제로 사람들은 그걸 쉽게 발음하더군요. 나는 CCS 처럼 약자를 만들고 싶지 않았습니다. 뭔가 순수한 이름을 짓고 싶었습니다.​2​

π-calculus는 CCS와 매우 유사하며 매우 간결하다. π-calculus의 주요 수식은 다음과 같다.

동시 수행(Concurrency)

두 개의 프로세스 P, Q가 동시적으로 수행되고 있음을 다음과 같이 표현한다.

P | Q
통신(Communication)

프로세스 사이의 상호작용 혹은 통신이 이루어지는 링크를 채널channel이라고 부른다. 프로세스는 이 채널을 통해서 연결되어 있는 다른 프로세스에게 어떤 데이터를 줄 수도 있고 받을 수도 있다.

채널의 이름을 c라고 했을 때 P라는 프로세스가 데이터를 받는 작업은 아래와 같이 표현할 수 있다. 여기서 x는 받은 데이터를 저장하는 변수의 이름이다.

c(x).P

채널의 이름을 c라고 했을 때 P라는 프로세스가 데이터를 내보내는 작업은 다음과 같이 표현할 수 있다. 여기서 y는 내보내는 데이터가 저장되어 있는 변수의 이름이다.

\bar c(y).P
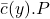
자신 복제(Replication)

프로세스 P가 자신을 복제하여 새로운 프로세스를 만드는 것은 다음과 같이 표현할 수 있다.

!P
새로운 이름 만들기

프로세스 P에서 사용할 새로운 이름을 만드는 것은 다음과 같이 표현할 수 있다. 새롭게 만들어진 이름은 채널로 사용된다.

(vx)P
프로세스 종료

프로세스가 종료되는 것은 0으로 표현한다.

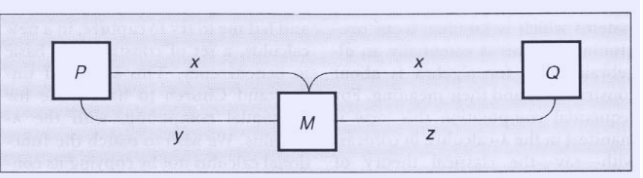
아래는 π-calculus를 사용하여 세 개의 프로세스 동시 수행을 표현한 사례이다.​7​

(vx) (\bar x(z).0
| x(y). \bar y(x). x(y). 0)
| z(v). \bar v(v). 0
  1. ​*​
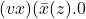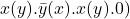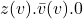
    출처: https://en.wikipedia.org/wiki/Robin_Milner
  2. ​†​
    출처: https://archive.cs.st-andrews.ac.uk/dls-archive/
  3. ​‡​
    공리(axiom)도 포함되는데 편의상 여기서는 생략하겠다.
  4. ​§​
    이는 merriam-webster 사전의 설명이다. (https://www.merriam-webster.com/dictionary/calculus) 이에 비해 위키피디아에서는 ‘계속 변화하는 것에 대한 수학적 연구’라고 정의하고 있다.

참고문헌

  1. 1.
    Milner R. Elements of interaction. ACM Turing Award Lectures.:1991. doi:10.1145/1283920.1283948
  2. 2.
    An Interview with Robin Milner. Electronic Notes in Theoretical Computer Science. Published online September 2006:3-36. doi:10.1016/j.entcs.2005.12.074
  3. 3.
    Milner R. Implementation and applications of Scott’s logic for computable functions. SIGPLAN Not. Published online January 1972:1-6. doi:10.1145/942578.807067
  4. 4.
    Gordon M, Milner R, Morris L, Newey M, Wadsworth C. A Metalanguage for interactive proof in LCF. Proceedings of the 5th ACM SIGACT-SIGPLAN symposium on Principles of programming languages  – POPL ’78. Published online 1978. doi:10.1145/512760.512773
  5. 5.
    Milner R, ed. A Calculus of Communicating Systems. Springer Berlin Heidelberg; 1980. doi:10.1007/3-540-10235-3
  6. 6.
    Gordon M. From LCF to HOL: A Short History. University of Cambridge; 2000:1-16.
  7. 7.
    π-calculus. Wikipedia. Accessed January 6, 2024. https://en.wikipedia.org/wiki/%CE%A0-calculus

(c) 이재범, 2024
이 콘텐츠는 대한민국 저작권법의 보호를 받습니다. 작성된 모든 내용의 권리는 저자에게 있으며, 저자의 동의 없는 사용은 금합니다. 본 콘텐츠의 일부 혹은 전체 내용을 무단으로 전재/복제/배포하거나 2차적 저작물로 재편집하는 경우, 법적 책임을 지게 됩니다.

1 2 3 4 5 6