스티븐 쿡

튜링상 관련 업적

스티븐 쿡의 가장 두드러진 업적은 NP-완전^complete 이론이다. 하지만, 그가 NP-완전이라는 이름을 짓지는 않았다. <정리 증명 절차의 복잡성>이라는 논문에서 그가 증명했던 것은, 어떤 특정 문제에 대한 답을 찾을 수 있다면 다른 많은 어려운 문제들의 답도 찾을 수 있다는 것이었다. 이 개념에 NP-완전이라는 이름을 붙인 이는 리처드 카프이다.

NP-완전

NP-완전^complete 이라는 개념이 중요하게 다뤄지는 이유는, 우리가 현실에서 접하는 문제 중 ‘효과적’인 해결책이 없는 문제들을 ‘대표’할 수 있기 때문이다. ‘효과적’이라는 표현과 ‘대표’한다는 표현을 좀 더 살펴보자.

‘효과적’이라는 표현을 구체적으로 설명하자면, 입력값의 크기가 아무리 커져도 답을 구하는 시간이 기하급수적으로^{exponentially} 늘어나지 않는 것을 말한다. 예를 들어, 비밀번호를 알아내야 하는 상황을 생각해 보자. 가장 무식하게 이 문제를 푸는 방법은 모든 가능한 숫자를 시도해 보는 것이다.

만약 비밀번호가 2자리라면 최악의 경우 100번(10² 번)을 해보면 된다. 그런데 비밀번호가 3자리라면 1,000번(10³ 번)을 해봐야 하고 비밀번호가 6자리라면 1,000,000번(10⁶ 번)을 해봐야 한다. 이를 수식으로 표현해 본다면, 입력값(십진수)의 자릿수를 n이라고 했을 때 답을 구하기 위한 시도 횟수는 최악의 경우 10ⁿ 번이 된다. 입력값의 크기를 나타내는 변수 n이 답을 구하기 위한 단계 횟수 공식의 지수^exponent 부분에 있음을 주목하자.

이제 곱셈 계산을 생각해 보자. 2자리 숫자를 서로 곱한다고 하면 우리가 흔히 쓰는 방법에서는 1자리 숫자 곱셈을 4번(2² 번) 한 후에 1자리 숫자 덧셈을 (최악의 경우) 7번 (2² + 2 + 2 – 1 번) 하게 된다. (덧셈의 경우 편의상 자리올림값이 포함된 세 개의 덧셈은 한 번으로 간주했다.)

    34
 x  96
 ------
    24
   18
   36
+ 27
-------
  3264 

      2775
  x   8888
  --------
        40
       56
      56
     16
       40
      56
     56
    16
      40
     56
    56
   16
     40
    56
   56
+ 16
------------
  24664200

4자리 숫자를 서로 곱한다면 1자리 숫자 곱셈을 16번(4² 번) 한 후에 1자리 숫자 덧셈을 (최악의 경우) 23번(4² + 4 + 4 – 1 번) 한다. 100자리 숫자를 곱한다면 1자리 숫자 곱셈을 10,000번(100² 번) 한 후에 덧셈을 10198번(100² + 100 + 100 – 1 번)한다. 따라서 곱셈 계산에서는 입력값의 자릿수를 n이라고 할 때 답을 구하기 위한 단계 횟수가 (최악의 경우) 2n² + 2n – 1 번이 되어서 입력값의 크기를 나타내는 변수 n이 단계 횟수 공식의 지수 부분에 나타나지 않는다. 곱셈의 경우처럼 알고리듬의 수행 단계 횟수를 나타내는 공식에서 입력값의 크기를 나타내는 변수가 지수^exponent에는 없고 밑^base에만 나타나면, 우리는 이 알고리듬의 수행 시간이 다항 시간^{polynomial-time}이라고 말한다.

자, 이제 다시 원래 하던 이야기로 돌아와 보자. ‘효과적’이라는 표현을 설명하다 보니 이렇게 먼 길을 돌아왔다. 어떤 문제에 대해서 ‘효과적’인 해결책이 있다는 것은 다항 시간 안에 답을 내는 알고리듬이 존재함을 의미한다. 이렇게 다항 시간 안에 답을 내는 알고리듬이 존재하는 문제들은 뭉뚱그려서 P 문제라고 부른다. P는 Polynomial-time을 가리킨다. 그렇다면 ‘효과적’인 해결책이 없는 문제들, 즉 다항 시간 안에 풀리는 알고리듬이 존재하지 않는 문제들은 무엇이라고 부를까? 이것들은 뭉뚱그려서 NP 문제라고 부른다. 잠깐! 여기서 굉장히 조심해야 한다. NP는 Not Polynomial-time을 의미하지 않는다. NP는 Nondeterministic Polynomial-time을 나타낸다. 이건 또 무슨 말인가. 이걸 굳이 해석하자면 ‘비결정적인 방법으로는 다항 시간’이라는 의미이다. 이에 대한 설명은 좀 뒤로 미루고 앞에서 하던 이야기를 마저 끝내겠다.

‘효과적’이라는 단어의 의미는 설명했는데, ‘대표’한다는 의미를 아직 설명하지 못했다. 바로 이 ‘대표’의 의미를 제시한 사람이 스티븐 쿡이다. 이 세상에는 많은 NP 문제들이 있다. 예를 들면 앞에서 언급한 비밀번호 알아내기를 포함하여 외판원 문제^{Travelling salesman problem}, 인수 분해^{integer factoring} 등이 있다. 그런데 이 많은 NP 문제들 중에서 어떤 문제는 좀 특별하다. 만약 그 문제가 다항 시간 내에 풀린다는 것이 증명되면 다른 모든 NP 문제들도 다항 시간 내에 풀림을 보장할 수 있다. 그래서 이 특별한 문제는 NP 문제를 ‘대표’하는 셈이 된다. 좀 다르게 설명한다면 이 ‘대표’문제는 다른 NP 문제들보다 어렵게 때문에 이 문제가 풀리면 결국 더 쉬운 다른 문제들은 자동으로 풀리는 결과를 가져온다.

이제 정리를 해보면, NP-완전에 해당하는 문제들은 NP 문제이면서 다른 NP 문제들보다 어려운 문제들을 의미한다.

비결정적 다항 시간

앞에서 NP 문제를 설명할 때 NP라는 표현은 Nondeterministic polynomial-time(비결정적 다항 시간)을 의미한다고 말했다. 이 표현을 좀 더 살펴보겠다. 다시 한번 강조하지만 NP는 Not Polynomial-time이 아니다.

비결정적 다항 시간이 의미하는 것은, 비결정적 튜링 기계^{nondeterministic Turing machine}를 사용하면 다항 시간 내에 답을 구할 수 있다는 것이다. 그렇다면 도대체 비결정적 튜링 기계는 무엇인가?

튜링 기계는 계산^computation이라는 것을 모델링하기 위해 앨런 튜링이 제안한 가상의 기계이다.^​5​ 이 기계는 테이프에 적힌 값을 읽은 후에 정해진 규칙에 따라 뭔가 작업을 한다. 그 작업은 테이프에 적힌 값을 변경하는 것일 수도 있고, 테이프를 전진시키거나 후진시키는 것일 수도 있다. 아울러 이 기계는 내부에 상태값을 관리하고 있어서 이 상태값에도 변화가 일어날 수 있다. 사실, 우리가 현실에서 사용하는 컴퓨터도 알고 보면 뭔가 입력을 받아서 일을 하는 블랙박스이므로 튜링 기계의 일종이다.

그런데 튜링 기계는 결정적 튜링 기계와 비결정적 튜링 기계로 나뉜다. 차이점은 테이프에 적힌 값을 읽은 후에 벌어지는 작업이 한 가지이냐 아니면 선택지가 존재하느냐이다. 전자의 경우가 결정적 튜링 기계이고 후자의 경우가 비결정적 튜링 기계이다. 비결정적 튜링 기계에서는 어떤 입력값(테이프에 적힌 글자)에 대해 복수 개의 결과(진행)들이 가능할 수 있다. 그렇다면 비결정적 튜링 기계는 어떤 입력값에 대해 선택지가 존재할 때 어느 것을 선택해야 할까? 그것은 정해져 있지 않으며 모든 선택지가 다 가능하다고 본다. 그렇기 때문에 임의로 하나의 선택지를 선택해 보고 그렇게 해서 답이 나오지 않으면 다시 다른 선택지를 선택하는 식으로 진행할 수 있다. 결국 될 때까지 해보는 식이다. 그러다가 답이 나오면 우리는 이 튜링 기계가 문제를 풀었다고 말한다.

그렇다면 ‘비결정적 튜링 기계를 사용하면 다항 시간 내에 답을 구할 수 있다’는 표현은 무슨 뜻일까? 비결정적 튜링 기계가 어떤 선택지를 결정했는데 다행히 그것이 정답으로 인도하는 경우였다면 답을 구하는 시간은 다항 시간에 가능하다는 의미이다. 하지만 선택지가 틀렸다면 다항 시간 내에 계산을 하더라도 답이 틀리게 되므로 다른 선택지를 시도해야 한다. 결국 ‘비결정적 튜링 기계를 사용하여 다항 시간 내에 답을 구할 수 있다’는 말이, 그 답을 구하는 데 걸리는 시간이 다항 시간 내에 가능하다는 의미는 아니다. 여러 입력값들에 여러 선택지가 가능하다고 하면 그 가능한 경우의 수를 다 시도해야 하므로 전체적으로 걸리는 시간은 다항 시간이 아닐 가능성이 높다.

NP 문제를 좀 다르게 표현하기도 한다. ‘다항 시간 내에 답을 검증할 수 있는 문제‘라는 식이다. 즉, 답에 대한 후보가 제공되면 이 답이 맞는지 틀리는지는 다항 시간 내에 확인할 수 있다는 것이다. 이와 대비되어 P 문제는 ‘다항 시간 내에 답을 찾을 수 있는 문제‘라고 표현하기도 한다.

충족 가능성 문제

스티븐 쿡은 NP 문제들이 몇 개의 문제들로 ‘대표’될 수 있음을 처음 보였다. ‘대표’한다를 수학적으로 표현하면 ‘환원 가능^reducible‘하다고 쓴다. 스티븐 쿡은 ‘환원 가능’의 의미를 다음과 같이 설명했다.

A 문제가 B 문제로 ‘환원 가능’하다는 말의 의미를 간단히 설명하자면, 어떤 기적이 일어나서 B 문제가 바로 풀리게 된다면 A 문제도 다항 시간 내에 답을 구할 수 있다는 것이다.^​3​

사실, 스티븐 쿡의 가장 큰 업적은 ‘환원 가능’함을 수학적으로 증명한 것이다. 그는 여러 어려운 문제들, 즉 다항 시간 내에 답을 구할 수 없는 문제들이 특정 몇 개의 문제들로 ‘환원 가능’함을 증명했다.

그가 찾은 NP-완전 문제에는 서브그래프 동형 문제^{subgraph isomorphism}, 항진식^tautology, 충족 가능성 문제^{satisfiability problem} 등이 있다.^​3​

스티븐 쿡이 찾은 NP-완전 문제 중 충족 가능성 문제는 흔히 3SAT 문제로 불린다. 이 문제는 다음과 같은 형태이다.

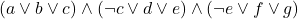
충족 가능성 문제의 답을 구한다는 것은, 이 논리 수식을 참으로 만들기 위한 변수의 값을 구하는 것이다. 위의 경우에는 수식을 참으로 만들기 위한 의 값을 구하는 일이 된다. 3SAT라고 부르는 이유는 괄호 안에 3개의 변수가 있기 때문이다. 참고로 괄호 안에 변수의 개수가 최대 2개이면 이 문제는 P 문제가 된다. 하지만 3개 이상이 되면 NP 문제가 된다.

P = NP ?

앞에서 여러 번 강조했듯이 NP는 Not P를 의미하지 않는다. NP는 ‘다항 시간 내에 답을 검증할 수 있는 문제’를 의미한다. 그렇다면 P에 해당하는 문제들은 NP에 해당하는가? 당연하다. 왜냐하면 P 문제들도 다항 시간 내에 답을 검증할 수 있기 때문이다.

하지만 NP 문제가 P에 해당할까? 답은 ‘아직 모른다’이다. 언뜻 보기에는 좀 의아하다. NP 문제는 답을 구하는 시간이 기하급수적으로 늘어난다고 했으므로 당연히 P가 아니어야 할 것처럼 보인다. 여기에는 함정이 있다. NP 문제의 답을 구하는 시간이 기하급수적으로 늘어난다고 우리가 말할 때는, 우리가 현재까지 알고 있는 해결책을 가정하고 이야기하는 것이다. 만약 어떤 천재가 혜성같이 나타나서 SAT 문제를 다항 시간 내에 풀어내는 알고리듬을 제시한다면 그때부터 SAT는 P 문제가 되는 것이다. 정리하자면 우리는 SAT 문제가 기하급수적인 시간을 쓰면 풀린다는 것을 알고 있지만, 다항 시간 내에 풀어내는 알고리듬이 존재하지 않음을 증명하지는 못한 상태이다.

과연 NP 문제가 P 문제에 해당하는지는 컴퓨터 과학뿐만 아니라 수학 분야에서도 초미의 관심사이다. 아직 추측만이 난무할 뿐이다. 그래서 이 문제는 클레이 수학연구소가 정한 7대 밀레니엄 문제에 포함되어 있다.^​6​

1 2 3 4