튜링상 관련 업적
인공지능 분야가 과학적 열정을 바칠 분야로 자리 잡는 데 기여했으며 휴리스틱 프로그래밍, 휴리스틱 검색, 수단-목표 분석, 귀납법 등을 개발하면서 이것들을 사용하여 흥미로운 문제를 해결할 수 있음을 보였다….
1975년 튜링상 선정 이유 중에서1
리스트 처리를 발명했으며, 소프트웨어 기술에 주요한 기여를 했음과 동시에, 컴퓨터가 그저 수치 데이터 처리기가 아니라, 기호를 사용한 구조체를 다루는 시스템이라는 개념을 발전시키는 데 크게 기여했다.
오늘날 우리는 컴퓨터가 다양한 용도로 사용되고 있음을 목도한다. 하지만 1955년에 컴퓨터는 수치 계산을 도와주는 도구에 불과했다. 아직 상용화된 전자식 컴퓨터도 없었고 프로그래밍을 쉽게 할 수 있는 고급 언어도 전무했다. 이런 상황에서 컴퓨터를 사용하여 ‘인간의 사고’를 흉내 내는 프로그램이 등장했으니 그야말로 센세이셔널했음은 당연했다. 수학 증명을 자동으로 해내는 기계를 접한 사람들에게 인공지능은 머지않은 미래로 여겨졌을 법하다.
로직 시어리스트
로직 시어리스트Logic Theorist는 <수학 원리>2에 나온 수학 정리를 자동으로 증명하겠다는 목적으로 만든 프로그램이다. 그러므로 범용의 인공지능 프로그램이 아니다. 하지만 여기에 사용된 여러 개념들은 후에 다른 인공지능 프로그램에 널리 사용되었다.
논리 기호학에서의 증명이란?
우선, 용어를 짚고 넘어갈 필요가 있겠다. 수학에는 정리theorem와 공리axiom가 있다. 공리는 그 자체로 자명하다고 판단되는 것을 말한다. 즉, 따로 증명할 필요 없이 참true이라고 받아들이는 것이다. 정리는 증명을 통해 참true임을 확인한 것을 말한다.
그렇다면 증명proof이란 무엇인가? 증명이란, 이미 참이라고 확인된 정보만을 사용해서 수학적 추론inference 절차를 거쳐 결과를 도출해내는 작업이다. 여기서 ‘이미 참이라고 확인된 정보’란 결국 공리 혹은 이미 증명된 정리들이다.
<수학 원리Principia Mathematica>는 기호 논리학을 다루고 있다. 로직 시어리스트에서 고려하는 수학적 추론 절차는 크게 3가지이다.10
- 대입Substitution : 변수 자리에 다른 수식expression을 넣는 것을 말한다. 예를 들어,
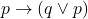 라는 수식이 참이라고 할 때,
라는 수식이 참이라고 할 때, 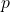 의 자리에
의 자리에 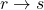 를 대입하여 나온
를 대입하여 나온 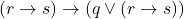 도 참이다.
도 참이다. - 제거Detachment :
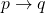 가 참이고
가 참이고 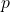 가 참이면,
가 참이면, 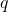 도 참이 되는 것을 말한다.
도 참이 되는 것을 말한다. - 연쇄Chaining:
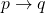 가 참이고
가 참이고  이 참이면,
이 참이면, 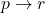 도 참이 되는 것을 말한다.
도 참이 되는 것을 말한다.
그렇다면 증명이란 무엇인지 다시 생각해보자. ![]() 라는 수식이 참임을 증명해야 한다고 해보자. 우리가 해야 할 일은, 이미 알고 있는 공리와 정리들에 대입, 제거, 연쇄라는 규칙을 적절한 순서로 적용함으로써
라는 수식이 참임을 증명해야 한다고 해보자. 우리가 해야 할 일은, 이미 알고 있는 공리와 정리들에 대입, 제거, 연쇄라는 규칙을 적절한 순서로 적용함으로써 ![]() 를 유도해낼 수 있음을 보여주는 것이다. 로직 시어리스트가 하는 일은 바로 이 대입, 제거, 연쇄의 적용순서sequence와, 사용되는 공리 및 정리들을 찾아내는 것이다.
를 유도해낼 수 있음을 보여주는 것이다. 로직 시어리스트가 하는 일은 바로 이 대입, 제거, 연쇄의 적용순서sequence와, 사용되는 공리 및 정리들을 찾아내는 것이다.
어떻게 동작하는가?
우리가 흔히 접하는 수학적 증명은 공리와 정리에서 출발하여 이러저러한 추론 절차를 거친 후에 최종 결론에 도달한다. 이에 비해 로직 시어리스트는 역추적working backward 방식으로 동작한다. 다시 말해, 증명해야 할 수식에서 시작해서 역방향으로 추론을 거슬러 올라가는데 공리와 정리만으로 표현이 가능해지면 증명이 완료된다.
예를 들어 설명해보겠다. ![]() 라는 수식을 증명해야 한다고 해보자. 로직 시어리스트는 대입, 제거, 연쇄의 순서로 차례차례 역방향 추론을 시도해본다.10
라는 수식을 증명해야 한다고 해보자. 로직 시어리스트는 대입, 제거, 연쇄의 순서로 차례차례 역방향 추론을 시도해본다.10
대입을 역방향으로 한다는 이야기는, 이미 주어진 공리와 정리 중에서 어떤 것에 대입을 적용하면 ![]() 가 만들어질지를 찾아본다는 이야기이다. 이는 두 가지 세부 단계로 구분되어 진행된다. 일단 유사한 것을 찾고similarity testing, 그다음에 맞춰보기matching 작업을 진행한다. 여기서 유사한 것을 찾는다는 것은 이미 알려진 공리와 정리 중에서 모양이 비슷한 것을 찾는다는 것이다.
가 만들어질지를 찾아본다는 이야기이다. 이는 두 가지 세부 단계로 구분되어 진행된다. 일단 유사한 것을 찾고similarity testing, 그다음에 맞춰보기matching 작업을 진행한다. 여기서 유사한 것을 찾는다는 것은 이미 알려진 공리와 정리 중에서 모양이 비슷한 것을 찾는다는 것이다.
‘비슷하다’는 것을 어떻게 판단해야 할까? 여기서 휴리스틱 방법론이 등장한다. ‘비슷함’을 정확하게 판단하기란 쉽지 않다. 그래서 로직 시어리스트에서는 수식의 모양을 보고 몇 가지 값을 계산해낸다. 예를 들어 몇 개의 변수가 있는지, 변수가 총 몇 번 나타나는지 등을 따져보고 이 값이 같으면 ‘비슷하다’고 본다. 사실 이렇게 계산한 값이 같다고 해서 ‘비슷하다’고 보아야 하는지에 대해서는 이견이 있을 수 있다. 하지만 항상 맞지는 않더라도 상당히 맞을 경우가 많기 때문에 사용하는 것이다. 바로 이것이 휴리스틱 방법론이다.
일단 비슷해 보이는 공리나 정리가 발견되었으면, 어떤 변수를 다른 수식으로 대입했을 때 우리가 증명하고자 하는 수식이 만들어질 수 있는지를 따져본다. 이것을 ‘맞춰보기matching‘라고 한다. 그런데 공리나 정리는 ![]() 등과 같은 연결자connective들에 의해 여러 단계의 구조를 가질 수 있다. 그래서 ‘맞춰보기’ 과정 중에, 하위 단계를 ‘맞춰보아야’ 하는 상황이 전개된다. 다르게 표현하자면, ‘맞춰보기’를 하는 서브루틴의 내부 동작 과정에서 다시 ‘맞춰보기’ 서브루틴을 호출해야 하는 상황이 발생한다. 다름 아닌 재귀적 호출recursion이다.
등과 같은 연결자connective들에 의해 여러 단계의 구조를 가질 수 있다. 그래서 ‘맞춰보기’ 과정 중에, 하위 단계를 ‘맞춰보아야’ 하는 상황이 전개된다. 다르게 표현하자면, ‘맞춰보기’를 하는 서브루틴의 내부 동작 과정에서 다시 ‘맞춰보기’ 서브루틴을 호출해야 하는 상황이 발생한다. 다름 아닌 재귀적 호출recursion이다.
![]() 에 대해 대입 역추론을 진행하게 되면, 일단 ‘유사한 것 찾기’를 통해
에 대해 대입 역추론을 진행하게 되면, 일단 ‘유사한 것 찾기’를 통해 ![]() 라는 기존의 정리theorem를 찾게 된다. <수학 원리>를 보면 이 정리는 이미 증명되어 제공된다.
라는 기존의 정리theorem를 찾게 된다. <수학 원리>를 보면 이 정리는 이미 증명되어 제공된다. ![]() 는
는 ![]() 로 교체할 수 있다. 왜냐하면 <수학 원리>에서
로 교체할 수 있다. 왜냐하면 <수학 원리>에서 ![]() 는
는 ![]() 와 동일하다고 정의definition되어 있기 때문이다. 이제 맞춰보기 과정을 통해
와 동일하다고 정의definition되어 있기 때문이다. 이제 맞춰보기 과정을 통해 ![]() 자리에
자리에 ![]() 를 대입하면
를 대입하면 ![]() 가 만들어질 수 있음을 확인하게 된다.13
가 만들어질 수 있음을 확인하게 된다.13
대입을 통해서 적합한 증명 절차를 찾지 못하는 경우도 있다. ![]() 이라는 수식이 그 예이다. 이런 경우에는 제거를 시도해본다. 제거를 역방향으로 한다는 이야기는
이라는 수식이 그 예이다. 이런 경우에는 제거를 시도해본다. 제거를 역방향으로 한다는 이야기는 ![]() 를 증명해야 할 때,
를 증명해야 할 때, ![]() 가 참임을 알게 된다면
가 참임을 알게 된다면 ![]() 를 증명하는 것으로 넘어가게 됨을 의미한다.
를 증명하는 것으로 넘어가게 됨을 의미한다. ![]() 의 예에서는 이미 주어진 공리 및 정리 중에서
의 예에서는 이미 주어진 공리 및 정리 중에서 ![]() 기호의 오른쪽이
기호의 오른쪽이 ![]() 의 형태인 것들을 찾는다. 이 과정은 앞에서 설명한 ‘유사한 것 찾기’와 ‘맞춰보기’가 동일하게 벌어진다. <수학 원리>에서는
의 형태인 것들을 찾는다. 이 과정은 앞에서 설명한 ‘유사한 것 찾기’와 ‘맞춰보기’가 동일하게 벌어진다. <수학 원리>에서는 ![]() 라는 정리가 이미 증명되어 있다. 로직 시어리스트는 이 정리에서
라는 정리가 이미 증명되어 있다. 로직 시어리스트는 이 정리에서 ![]() 오른편에 있는
오른편에 있는 ![]() 가 주어진 수식과 동일한 구조임을 알아낸다. 따라서 이제 증명 작업은,
가 주어진 수식과 동일한 구조임을 알아낸다. 따라서 이제 증명 작업은, ![]() 의 왼편에 있는
의 왼편에 있는 ![]() 를 증명하는 일로 넘어가게 된다. 주어진 수식의 값으로 변수를 대입해보면
를 증명하는 일로 넘어가게 된다. 주어진 수식의 값으로 변수를 대입해보면 ![]() 을 증명하는 일이 된다. 다행히 이 수식은 대입만으로 증명해낼 수 있다. 왜냐하면
을 증명하는 일이 된다. 다행히 이 수식은 대입만으로 증명해낼 수 있다. 왜냐하면 ![]() 라는 정리가 이미 있기 때문이다.13
라는 정리가 이미 있기 때문이다.13
탐색 공간
주어진 수식에서 출발하여 어떤 정리와 공리로 역추적하는 과정은, 트리tree를 탐색search하는 모양이다.
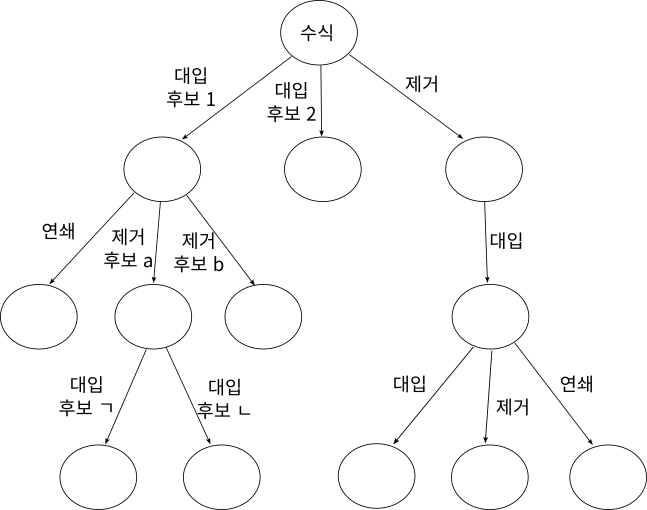
주어진 수식은 트리의 뿌리에 해당한다. 앞에서 언급했듯이 로직 시어리스트는 대입, 제거, 연쇄의 방법을 사용해서 추론 과정을 역추적한다. 이때 대입, 제거, 연쇄가 적용되는 과정이 단 한 개만 있으라는 법은 없다. 예를 들어 대입의 과정에서 ‘유사한 것 찾기’에 의해 후보로 선정될 수 있는 공리 혹은 정리가 여러 개 있을 수 있으며, 제거에서도 마찬가지이다. 이렇듯 여러 가능성이 존재하고, 만약 어느 하나의 가능성을 선택하여 다음 역추론 단계를 하였을 때 역시 거기서도 여러 가능성이 존재할 수가 있다. 따라서 원하는 결과에 도달하기까지 여러 번 선택의 갈림길에 처할 가능성이 있다.
로직 시어리스트는 휴리스틱을 이용해서 가장 답에 가까울 것으로 판단되는 것을 고른다. 그런 점에서 로직 시어리스트는 최상 우선 탐색Best first search이라고 볼 수 있다.1
이렇듯 시작점이 주어지고 어떤 규칙들에 의해서 다양한 상황이 전개되는(혹은 상태로 전이되는) 형태를 문제 공간problem space 혹은 탐색 공간search space이라고 부른다. 인공지능의 많은 문제들은 결국 이런 문제 공간 내에서 정답 지점까지 가는 경로를 알아내는 것이다. 로직 시어리스트는 문제 공간에서의 탐색을 최초로 구현한 인공지능 프로그램이었다.



답글 남기기