에드스거 다익스트라

튜링상 관련 업적

다익스트라에 앞서서 튜링상을 수상한 인물들의 면면을 보면 모두 젊은 시절에 한 가닥씩 프로그래밍 실력을 날렸음을 확인할 수 있다. 하지만 프로그래밍을 하나의 연구 분야로 우뚝 세운 이는 다익스트라였다고 보아도 과언이 아닐 듯싶다. 그 이전까지만 해도 산술 연산의 조합으로 여겨졌던 프로그래밍을, 독창적 알고리듬의 우아한 구현으로 승화시켰다.

튜링상 선정 이유에서 분명하게 언급되었듯이 그로 인해 프로그래밍은 지적인 도전 과제로 자리 잡았고, 프로그램을 설계하기 위해 우리가 어떤 것을 알아야 하는지가 분명해졌다. 아울러 그에게 프로그래밍은 우아한 창조적 활동이어야 했다. 프로그램은 간결해야 했으며 구조적으로 틀이 잡혀 있어야 했다. 그리고 프로그램의 정확성은 오류를 해결하는 식이 아니라, 미리 검증되어야 했다.

최단 경로 알고리듬

앞에서 언급했듯이 최단 경로 알고리듬은 컴퓨터 시연을 위해서 급조(?)된 알고리듬이었지만, 후에 엄청나게 유용하게 사용되었다. 네트워크상에서 두 지점을 연결하는 가장 빠른 경로를 요구하는 응용은 생각보다 많다. 대표적인 것은 차량용 내비게이션이다. 내가 있는 위치에서 목적지까지 가장 빠른 길을 찾을 때 최단 경로 알고리듬이 사용된다. 그리고 일반인에게는 드러나 있지 않지만 아주 중요하게 사용되는 분야가 있다. 우리가 인터넷에서 데이터를 주고받을 때도 가장 빠른 경로를 찾기 위해 이 알고리듬이 사용된다.

다익스트라의 최단 경로 알고리듬은 아래의 예를 보면 이해할 수 있다. 이 그림에서 주어진 문제는 1번 노드에서부터 5번 노드까지 가장 짧은 경로를 찾는 것이다.

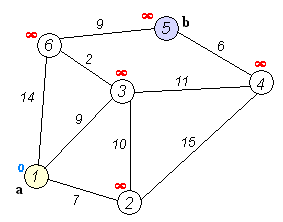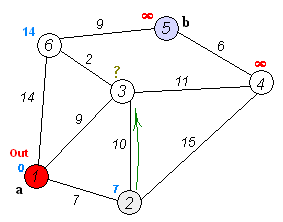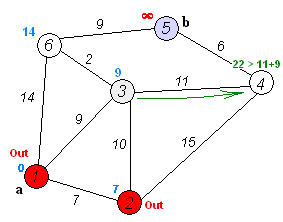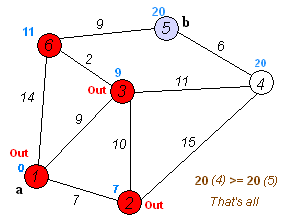
한 가지 주의할 점이 있다. ‘짧은 경로’라는 것이 그저 거치는 간선^edge의 개수가 가장 작은 것을 의미하지 않는다는 점이다. 사실은 ‘최소 비용 경로’라고 표현하는 편이 정확할 듯싶다. 위의 그림을 보면 각 간선에는 숫자가 매겨져 있다. 간선을 사용할 때 발생하는 비용을 의미한다. 현실을 생각하면 이런 비용은 당연하다. 예를 들어 서울에서 부산까지는 경부고속도로, 서울에서 인천까지는 경인고속도로라는 간선이 각각 존재하는데 ‘거리’와 ‘시간’이라는 측면에서 차이가 존재한다.

따라서 위의 그림에서 우리가 해야 할 일은 1번 노드에서 5번 노드까지 연결해주는 경로들 중에서 가장 비용의 합이 작은 경로를 찾는 것이다.

기본적인 아이디어는 1번 노드에서 갈 수 있는 경로를 차례로 뒤지면서 계속 누적 비용을 확인하는 것이다. 만약 1번 노드에서 5번 노드까지 연결되는 경로가 한 개만 존재한다면 아주 싱거운 일이 될 것이다.(사실 그렇다면 굳이 이런 알고리듬을 쓸 필요도 없다.) 하지만 복잡한 네트워크에서는 두 노드를 연결하는 경로가 여러 개일 가능성이 높다. 위의 예에서도 1번 노드에서 5번 노드까지 이어지는 경로는 1-6-5, 1-3-6-6, 1-3-4-5, 1-2-3-4-5 등이 있다.

3번 노드가 여러 경로에서 중복해 나타남에 유의하자. 즉 1번 노드에서 3번 노드까지 가는 경로가 여러 개 존재할 수 있다는 것이다. 1번 노드에서 3번 노드까지 누적한 비용의 값은 경로마다 다를 수 있다. 그중에서 가장 작은 값의 경로를 기억하는 것이 이 알고리듬의 핵심이다.

알고리듬의 동작은, 먼저 시작점 노드의 저장 누적 비용을 0으로, 이를 제외한 나머지 모든 노드의 저장 누적 비용을 ‘무한대’로 초기화한 후 시작된다. 1번 노드와 직접 연결되는 노드들마다 경로 누적 비용을 계산한다. 경로의 누적 비용은 그 경로의 시작점에 있는 노드의 누적 비용에 경로가 가진 비용을 더한 것이다. 경로 누적 비용이 계산되면 경로 끝의 노드에 저장된 기존의 누적 비용과 비교하여 작은 값으로 교체 저장한다. 예를 들어 2번 노드를 생각해보면 1번 노드의 저장 누적 비용은 0으로 초기화되어 있었으므로 경로 누적 비용은 0+7=7이 된다. 이렇게 계산된 경로 누적 비용과 2번 노드에 저장되어 있던 누적 비용을 비교해서 작은 쪽을 선택한다. 2번 노드에 저장되어 있던 누적 비용은 무한대였으므로 이제 7이 새로운 누적 비용이 된다. 이런 식으로 3번 노드에는 9, 6번 노드에서 14가 누적 비용으로 저장된다.

이제 2, 3, 6번 노드 중에서 저장 누적 비용이 가장 작은 2번 노드가 새로운 출발점이 된다. 2번 노드에 직접 연결된 노드 중에서 0번 노드는 이미 지나왔으므로 제외된다. 4번 노드의 경우는 앞에서와 마찬가지 방식으로 처리하면 15가 누적 비용으로 저장된다. 그런데 3번 노드의 경우는 새롭게 계산한 경로 누적 비용이 17인 것에 반해, 저장된 누적 비용은 9이므로 기존의 저장된 값이 더 작다. 따라서 2번 노드를 통한 경로는 제외되고 원래 저장되었던 값이 유지된다.

이제 3번 노드가 새로운 출발점이 된다. 직접 연결된 노드 중 이미 지나온 1번, 2번 노드는 제외된다. 6번 노드로의 누적 경로 비용은 11, 4번 노드로의 누적 경로 비용은 20이다. 둘 다 6번 노드와 4번 노드에 저장된 누적 비용보다 작으므로 기존의 값을 쫓아내고 저장된다.

이제 6번 노드가 새로운 출발점이 된다. 직접 연결된 노드 중에서 1번과 3번 노드는 제외된다. 5번 노드까지의 경로 누적 비용은 14+9=23이 되고, 5번 노드에 저장되어 있던 누적 비용은 무한대이므로 23이라는 값이 새롭게 저장된다.

경로 계산이 끝나지 않은 노드는 4번 노드가 남아 있다. 4번 노드에서 5번 노드까지의 경로 누적 비용은 20+6=26이므로 5번 노드에 저장되어 있던 23보다 크다. 따라서 기존의 저장된 누적 비용 23이 그대로 유지된다.

이제 지금까지의 설명에서 생략했던 내용을 밝힐 때가 되었다. 각 노드에서 경로 누적 비용을 갱신할 때는 그 비용을 구성하는 경로의 정보도 저장한다. 즉, 앞의 예에서 맨 처음 1번 노드에서 2번 노드로의 경로 누적 비용을 계산하고 그 결과값인 7을 2번 노드에 저장할 때는, 이 누적 비용이 1번 노드를 기준으로 계산되었음을 함께 저장한다. 따라서 우리가 5번 노드에서 최종적으로 20이라는 누적 비용을 결정하게 되면, 이제 이 20이라는 값이 6번 노드를 통해 계산되었음을 확인할 수 있다. 6번 노드에서는 14라는 누적 비용이 3번 노드를 통해 계산되었음을 확인할 수 있다. 3번 노드에서는 9라는 누적 비용이 1번 노드를 통해 계산되었음을 확인할 수 있다. 이렇게 역추적을 하게 되면 1번 노드에서 5번 노드까지의 최단 경로(최소 비용 경로)가 1-3-6-5임을 알게 된다.

최소 신장 트리 알고리듬

최소 신장 트리 알고리듬은 다익스트라가 처음 만든 알고리듬이 아니다. 1930년에 체코슬로바키아의 수학자이던 보이체 햐르니크^{Vojtěch Jarník}가 처음 발명했다고 한다. 하지만 세상에 알려지지 않았다. 그러다가 1957년에 벨 연구소의 연구원이던 로버트 프림이 같은 알고리듬을 스스로 고안해냈고, 2년 후인 1959년에 네덜란드의 수학 센터에 있던 다익스트라가 역시 스스로 생각해냈다.

최소 신장 트리 알고리듬을 이해하려면 먼저 신장 트리^{spanning tree}가 무엇인지 알아야 한다. 여기서 말하는 트리^tree는 자연에 있는 나무를 의미하는 것이 아니라, 수학의 그래프 이론에 나오는 하나의 그래프 형태이다. 수학에서 말하는 그래프^graph는 복수 개의 노드^node들이 간선^edge으로 서로 연결되어 있는 형태를 말하는데, 그중에서도 노드 사이를 연결해주는 경로가 항상 한 개만 존재하는 형태를 ‘트리’라고 한다.

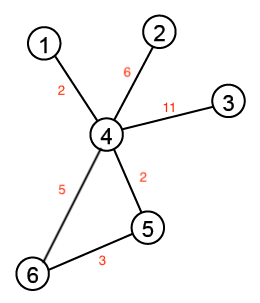
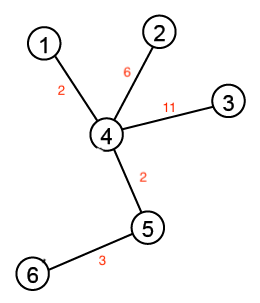
신장 트리는, 어떤 그래프가 주어졌을 때 일부 간선을 제거해서 트리 형태로 뽑아낸 것을 나타낸다. 위의 예에서 오른쪽의 트리는 왼쪽의 그래프에서 4번 노드와 6번 노드 사이의 간선을 제거해서 만들어 낸 신장 트리이다. 왼쪽 그래프에서 만들어 낼 수 있는 신장 트리는 한 개만 있는 것이 아니다. 4번과 5번 노드 사이의 간선을 지워도 되고, 5번과 6번 노드 사이의 간선을 지워도 된다. 하지만 4번과 3번 사이의 간선을 지운 것은 신장 트리가 아니다. 왜냐하면 그렇게 되면 3번 노드가 완전히 분리되기 때문이다.

위의 예에서 볼 수 있듯이 그래프에서 찾아낼 수 있는 신장 트리는 여러 개가 있을 수 있다. 그중에서 간선의 비용을 합한 것이 가장 작은 신장 트리를 최소 신장 트리라고 부른다. 최소 신장 트리도 많은 응용을 가지고 있다. 예를 들어 여러 도시를 연결하는 도로망을 건설한다고 했을 때 최소 신장 트리를 찾아내면 건설비를 최소화할 수 있다. 다익스트라의 경우도 하드웨어를 구현할 때 여러 부품들을 하나로 묶어 주는 전선의 길이를 최소화하기 위해 최소 신장 트리 알고리듬을 고안했다.

1 2 3 4 5 6