튜링상 관련 업적

계산 복잡도 이론 분야의 시작을 알리면서 후대에 지대한 영향을 준 논문을 발표함

1993년 튜링상 선정 이유​7​

곱셈은 덧셈보다 얼마나 더 어려울까?

수학 문제를 풀다 보면 난이도라는 것이 있다. 어떤 문제는 쉽고 어떤 문제는 어렵다. 굳이 수학으로 한정할 필요도 없다. 살다 보면 어떤 일은 쉽고 어떤 일은 어렵다. 우리는 감각적으로 그 차이를 느낀다. 그 어려움을 정량적으로 표현하기는 쉽지 않다. 입시용 수학 문제집 같은 것을 보면, 난이도를 상, 중, 하로 표현하기도 하는데 이것은 정성적인 표현이다. ‘난이도 12의 문제’, ‘난이도 87의 문제’와 같은 식으로 난이도를 측정하기란 쉬운 일이 아니다.

‘계산 복잡도computational complexity‘는 말 그대로 계산이 얼마나 복잡한지를 나타내는 지표이다. 이 용어를 처음 사용한 이가 유리스 하트마니스와 리처드 스턴즈였다. 그들에게 튜링상을 안겨 준 논문인 <알고리듬의 계산 복잡도에 관하여>​6​에서 처음 이 용어를 사용했다. 그 논문 이후로 이 용어는 하나의 분야로 자리매김했다.

이런 용어를 사용하지는 않았지만 계산이 얼마나 복잡한지를 따져보는 작업은 이미 있었다. 1960년에 마이클 래빈은 <함수 계산의 난이도와 재귀적 집합의 계층>​8​이라는 논문에서 함수 계산의 난이도degree of difficulty를 따져 보았다.​9​ 하지만 그는 정성적인 비교를 했을 뿐, 정량적인 지표를 제시하지는 않았다.

계산 복잡도 클래스

하트마니스와 스턴즈가 계산 복잡도를 정량화했다고는 하지만, 여기에는 약간의 함정이 있다. 그들의 방법을 쓴다고 해서 어떤 계산의 복잡도가 하나의 수식으로 ‘짜잔’하고 나오지는 않는다. 사실 그들이 한 일은 계산 복잡도 클래스computational complexity class라는 것이다.

계산 복잡도 클래스란, 같은 계산 복잡도를 가지는 계산들의 집합으로 이해할 수 있다. 컴퓨터가 수행하는 프로그램 혹은 계산은 다양할 터인데, 그것들 중에는 같은 계산 복잡도를 가지는 것들이 있다. 그렇게 같은 계산 복잡도를 가지는 계산들은 같은 ‘계산 복잡도 클래스’에 속해있다는 식으로 표현한다.

이것만 놓고 보면 좀 실망감이 들 수도 있겠다. ‘이게 무슨 정량적인 방법인가?’라고 의문을 던질 수도 있다. 그런데 하트마니스와 스턴즈는 시간함수time function라는 것을 도입했다.

시간함수

계산 복잡도에서 말하는 시간함수 T(n)은 세 가지 조건을 만족하는 함수이다.

  • 단조 증가monotone increasing함수, 즉 T(n) \leqq T(n+1)
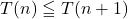
  • 정수값을 받아서 정수값을 출력
  • 모든 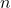n의 값에 대해서 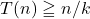T(n) \geqq n/k를 만족시키는 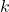k가 있음

시간함수는 계산 복잡도 클래스를 구별하는 데 사용된다. 만약 어떤 계산이 입력값 n에 대해서 T(n) 시간 안에 끝날 수 있다면 그 계산은 T-계산가능computable이라고 표현되며, 아울러 계산 복잡도 클래스 S_T에 포함된다고 말한다.

계산 복잡도 클래스 S_T란 ‘T-계산가능’한 모든 계산의 집합이다. 다르게 표현한다면, 입력의 크기가 n이고 단조 증가함수 T(n)에 대해, T(n) 내에 계산 가능한 모든 알고리듬들의 집합이다.

약간 귀신 씻나락 까먹는 소리처럼 들릴 수도 있겠다. 이것을 그래프로 그려 보면 조금 이해가 쉽다.

그림 1. 입력 크기에 따른 실행시간 변화의 예

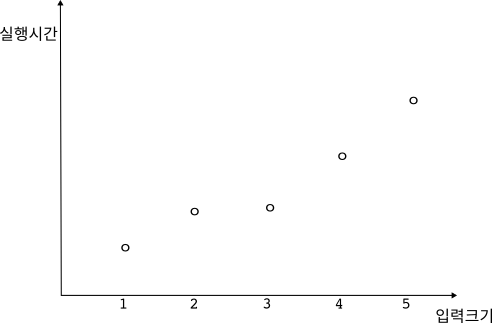
위의 그림 1은 어떤 계산에 대해 입력 크기에 따른 실행시간 값을 보여주고 있다. 동그라미 점이 계산의 실행시간을 표시한 것이다. 입력의 크기가 1에서 5로 증가하면서 실행시간도 단조증가하고 있다. 상식적으로, 입력의 크기가 커지면 계산 시간이 늘어남은 당연하다.

그런데 입력 크기에 따른 실행시간의 변화를 정확하게 수식으로 표현한다면 좋겠으나, 쉽지 않은 일이다. 만약 단순한 수식을 위해서 정확도를 조금 포기한다면 어떨까? 단순한 수식을 썼을 때 얻어지는 실행시간의 근사치가 실제 실행시간보다 작지만 않다면 그 수식이 틀렸다고 말할 수는 없을 것이다. 이제 그림 2를 보도록 하자.

그림 2. 시간함수의 예

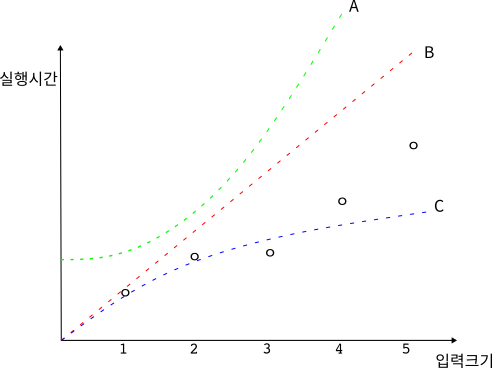
그림 2는 그림 1에 세 개의 그래프 선을 추가한 것이다.

빨간색 선 A와 초록색 선 B는 모두 동그라미 점 위를 지나는 반면에 파란색 선 C는 일부 동그라미 점의 아래를 지나고 있다. 완벽하지는 않지만 A와 B는 이 계산의 실행시간을 묘사하는 용도로 사용할 수 있다.

빨간색 선, 초록색 선, 파란색 선은 시간함수의 예이며 각각 하나의 계산 복잡도 클래스를 나타낸다. 위의 그림에서 해당 계산은 시간함수 A와 시간함수 B에 대해서는 ‘계산가능computable‘하다. 다시 말하자면 시간함수 A와 시간함수 B의 계산 복잡도 클래스에 포함된다. 하지만 파란색 선으로 표시된 시간함수 C는 입력 크기 4와 5에서 실제 계산 시간보다 작은 값을 가지므로 이 계산의 계산 복잡도 클래스가 될 수 없다.

그래프를 보면 시간함수의 용도를 이해할 수 있다. 시간함수란, 대상이 되는 계산의 실행시간들에 대한 경계boundary를 정량적으로 규정하는 일을 한다. 그리고 이 경계 내에서 실행이 끝날 수 있는 계산들을 모두 뭉뚱그려서 계산 복잡도 클래스라고 부르는 것이다.

계층성

위의 그래프에서 시간함수 A와 시간함수 B는 다른 형태를 보여주고 있다. 시간함수 A는 시간함수 B보다 더 급격하게 실행시간이 증가하는 특성을 보여준다. 이렇듯 시간함수 사이에는 증가율의 차이가 있을 수 있기 때문에 각 시간함수에 해당하는 계산 복잡도 클래스의 크기도 달라진다.

위의 그래프에서 시간함수 A의 계산 복잡도 클래스는 시간함수 B의 계산 복잡도 클래스를 포함하면서 더 크다. 즉, 어떤 계산은 시간함수 B의 계산 복잡도 클래스에는 포함되지 않지만 시간함수 A의 계산 복잡도 클래스에는 포함될 수 있는 것이다. 이를 계층성hierarchy이라고 부르며 다음과 같이 표현한다.

시간함수 U와 T에 대해

    \[\inf_{n \to \infty} {{T(n)^2} \over {U(n)}} = 0\]

이면 S_U에는 속하지만 S_T에는 속하지 않는 계산 \alpha가 존재한다.

이를 다르게 표현한다면, 위의 조건이 만족된다면 S_T \subset S_U라는 말이다. 그림을 보면 더 이해하기 쉽다. 앞의 그림 2를 보면 선 A는 선 B 보다 위쪽에 위치한다. 따라서 선 B가 포함하지 못하는 계산들을 선 A는 포함할 수 있음을 알 수 있다.

왜 이렇게 추상적인가?

하트마니스와 스턴즈의 계산 복잡도를, 후에 나온 다항 시간 복잡도polinomial time complexity나 점근적 복잡도asymtotic complexity와 혼동하기 쉽다. 어찌 보면 다항 시간 복잡도와 점근적 복잡도가 두 사람의 이론에 들어 있었던 듯하지만 이를 명시적으로 언급하지는 않았다. 그렇게 된 이유 중 하나는, 두 사람이 사용한 모델이 추상적이었기 때문이라고 추측된다.

두 사람은 복수 개의 테이프를 가지는 튜링 기계에서 이론을 전개했다. 튜링 기계에서 이루어지는 계산은 일종의 문자열 해석string interpretation이다. 튜링 기계는 모든 계산을 표현할 수 있다고 하는데, 모든 계산이 문자열 해석으로 변환 가능하다고 보기 때문이다. 아무튼 튜링 기계는 추상적인 기계이기 때문에 실행 시간이라는 개념은 없고, 실행 단계 횟수number of steps를 따진다.

따라서, <알고리듬의 계산 복잡도에 관하여>라는 논문을 보면, 계산 복잡도를 논할 때 특정 계산 알고리듬을 사례로 사용하지 않는다. 그저 튜링 기계에서 테이프 입력을 처리하는 상황의 어려움을 수학적으로 따질 뿐이다.

1 2 3 4