존 코크

컴파일러 최적화

스트레치 컴퓨터 프로젝트에서 컴파일러의 중요성을 실감했던 존 코크는 ACS-1 컴퓨터 프로젝트에서 본격적으로 컴파일러 기법 개발에 몸담았다. 컴파일러는 몇 개의 단계로 구성되는데 그가 관심을 가진 것은, 컴파일러의 결과물인 기계어 코드 덩어리를 최적화해서 성능을 극대화하는 것이었다. 수행되는 컴퓨터 하드웨어의 특성에 따라 최적화하는 방법은 달라질 수도 있었다.

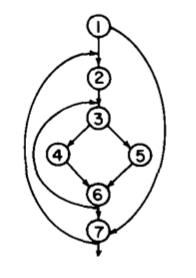
존 코크의 컴파일러 최적화는 그가 프랜시스 앨런과 함께 개발한 흐름 분석^{flow analysis}에 바탕을 둔다. 흐름 분석은 제어 흐름 분석과 데이터 흐름 분석으로 나뉜다. 제어 흐름 분석은 프로그램의 수행 흐름을 그래프 형태로 추출해낸다. 그렇게 구한 제어 흐름 그래프를 바탕으로 변수의 변화와 사용을 추적하는 것이 데이터 흐름 분석이다.^​9​

공통 부분식 제거

포트란 언어와 같이 고급 언어로 작성한 프로그램 코드를 컴파일할 때, 코드 한 줄씩 충실하게 기계어 코드로 변환하다 보면 사실상 동일한 일을 하는 기계어 코드가 중복해서 나타날 수 있다. 다음의 예를 보자.^​10​

A(I, J) = B(I, J)

포트란으로 작성된 위의 코드는 B라는 배열의 값을 A라는 배열로 복사하는 일을 한다. 만약 A와 B 배열이 25 x 25 크기의 2차원 배열이라고 가정한다면 위의 코드는 컴파일러에 의해 다음과 같이 기계어 코드로 바뀔 수 있다. (편의상 기계어 코드를 직접 쓰지 않고 이해하기 편한 방식으로 표기했다.)

K = I * 25
L = K + J
M = Address(B) + L
Load from (M)
N = I * 25
O = N + J
P = Address(A) + O
Store into (P)

위의 코드를 보면 N은 K와 동일하고 O는 L과 동일할 수 있음을 알 수 있다. 따라서 N과 O는 모두 다음과 같이 생략할 수 있다.

K = I * 25
L = K + J
M = Address(B) + L
Load from (M)
P = Address(A) + O
Store into (P)

공통 부분식^{common subexpression} 제거는 위의 예와 같이 가까운 범위내에서 일어날 수도 있지만, 훨씬 더 큰 범위에서도 가능하다. 하지만 범위를 넓힐수록 난이도가 증가한다. 존 코크는 데이터 흐름 분석^{data flow analysis}이라는 방법을 고안하여 여기에 활용했다.^​9​

연산 강도 경감

연산 강도^{Operator Stength}란 연산을 처리하기 위한 비용, 즉 시간과 저장 공간을 의미한다. 따라서 같은 일을 하는데 연산 강도가 낮을수록 더 좋다. 예를 들어 제곱 계산보다는 곱셈이 연산 강도가 낮고, 곱셈보다는 덧셈이 연산 강도가 낮다. 다음과 같은 코드가 있다고 해보자.^​11​

for (i = 0; i < 50; i++) {
    SUM = SUM + A[i][3];
}

A라는 2차원 배열에서 각 행의 4번째 값을 모두 더하는 일을 한다. A 배열의 크기는 50 x 50이라고 가정하자. 컴파일러를 사용하면 다음과 같은 코드가 생성될 수 있다. (편의상 기계어를 쓰지 않고 이해하기 편한 방식으로 표기했다.)

     i = 0
LOOP:
     m = i * 50 + 3
     n = indexed load (A, m)
     SUM = SUM + n
     i = i + 1
     IF (i < 50) GO TO LOOP

LOOP 안에서 i * 50 + 3은 배열의 원소에 접근하기 위해 흔히 사용하는 방식이다. 하지만 곱셈은 연산 강도가 높다. 반복문 안에 연산 강도가 높은 코드가 있으면 전체적인 성능이 저하된다. 이것을 다음과 같이 덧셈으로 바꾸게 되면 연산 강도가 경감된다.

     i = 0
     p = 50
LOOP:
     q = p + 3
     n = indexed load (A, q)
     SUM = SUM + n
     i = i + 1
     p = p + 50
     IF (i < 50) GO TO LOOP

존 코크는 흐름 분석을 통해서 곱셈 연산을 덧셈 연산으로 바꾸는 방법을 제시했다.^​11​

레지스터 할당

폰 노이만 구조에서 메모리 접근 시간은 컴퓨터 시스템의 성능을 좌우한다. 메모리 접근 시간이 빠를수록 성능은 높아진다. 그런데 폰 노이만 구조가 명시적으로 정의하고 있지는 않지만 메모리처럼 사용되는 구성 요소가 있다. 레지스터^register이다. 레지스터는 산술논리연산 작업의 입력단과 출력단에서 데이터를 임시 보관하는 일을 한다. 레지스터는 메모리가 아니므로 번지를 가지지 않는다. 대신에 이름을 갖는다. 이름을 붙이는 방법은 컴퓨터 업체마다 다르지만 흔히 R1, R2 식의 이름을 가진다.

레지스터는 메모리 소자가 아니라 일반 전자 회로이다. 따라서 매우 속도가 빠르다. 메모리를 이렇게 레지스터처럼 만들면 좋겠지만 그렇게 되면 비용이 너무 커져서 감당이 되지 않는다.

고급 언어로 작성한 코드를 컴파일러가 기계어 코드로 변환하면 자연스럽게 레지스터를 사용할 수밖에 없다. 왜냐하면 기계어 자체가 레지스터를 사용하게 되어 있기 때문이다.

다음과 같은 코드를 컴파일한다고 가정해 보자.

int i, j;
i = j + 200;

컴퓨터 프로그램에서 변수란, 기본적으로 메모리에 존재하는 어떤 값이다. 따라서 변수에는 반드시 메모리 번지라는 속성이 따라올 수밖에 없다. 실제 번지값은 알 수 없다. 그것은 컴파일러 및 운영체제에 의해 결정된다. 여기서는 i라는 변수의 주소가 300, j라는 변수의 주소가 100이라고 가정해 보겠다. 그러면 위의 코드는 아래와 같은 어셈블리어로 변환될 수 있다.

ADD @100 200 @300

이 어셈블리어 코드에는 레지스터가 사용되고 있지 않다. 이제 원본 코드를 아래와 같이 조금 확장해 보자.

int i, j, k;
i = j + 200;
k = i + 50;

위의 코드를 어셈블리어로 변환하면 다음과 같을 수 있다. 변수 k의 주소는 400이라고 가정한다.

ADD @100 200 @300
ADD @300 50 @400

그런데 변수 i(주소 300)의 값을 메모리에 썼다가 다시 읽지 않고 다음과 같이 레지스터에 보관하면 어떨까?

ADD @100 200 R1
ADD R1 50 @400
STORE R1 @300

이렇게 하면 메모리 접근이 한 번 감소하기 때문에 성능이 향상될 수 있다. 즉, 계산에 사용되는 데이터가 최대한 레지스터에 머무르게 할 수 있다면 메모리 접근 횟수가 줄어들게 되므로 훨씬 유리하다.

레지스터 할당^{register allocation}이란 컴파일러가 기계어 코드를 생성할 때 산술연산논리 연산의 결과값을 저장할 레지스터를 선택하는 과정을 의미한다. 위의 예에서는 R1이라는 레지스터를 할당했다.

레지스터 할당이 쟁점이 되는 이유는, 컴퓨터 프로세서에 여러 개의 레지스터가 있기 때문이다. 그래서 어떻게 레지스터를 할당하느냐에 따라 성능의 차이가 생긴다. 제일 최적의 레지스터 할당은, 메모리 접근을 최소화하는 것이다. 안타깝게도 레지스터 할당은 NP-완전 문제이다. 즉, 다항 시간 안에 최적의 답을 구하는 알고리듬이 아직 존재하지 않는다.

존 코크의 연구팀은 레지스터 할당을 그래프 색칠하기^coloring 문제로 변환했다.^​12​ 레지스터 할당을 위한 그래프에서 각 노드는 프로그램에서 다루는 변수를 나타내고, 노드와 노드 사이의 변^edge은 해당 변수들이 동시에 사용되고 있음을 나타낸다. 따라서 변으로 연결된 노드들은 같은 레지스터에 할당할 수 없다.

상수 전파

상수는 고정된 값이기 때문에 기계어 코드에서도 그대로 사용이 가능하다. 만약 어떤 변수가 항상 고정된 값을 가지고 있음을 알아내기만 한다면 우리는 그 변수를 해당 상수로 교체할 수 있다. 대표적인 사례가 값이다.^​10​

float pi = 3.14159;
x = 2 * pi * y;

위와 같은 코드가 있다고 하자. 만약 pi 변수의 값이 바뀌지 않고 계속 끝까지 유지된다는 것이 확인된다면 위의 코드는 아래와 같이 바뀔 수 있다.

x = 6.28318 * y;

상수 교체가 아니라 상수 전파^{constant propagation}이라는 이름이 붙은 이유는 프로그램 내에 나타나는 어떤 변수를 완전하게 교체하는 것이 불가능할 때가 있기 때문이다.

int x = 1;
...
y = x * 10;
...
x = 2;
...
z = x * -10;
...

위와 같은 코드가 있다고 가정하자. 여기서 x의 값은 중간에 한 번 바뀐 후에 변하지 않는다고 하자. 그렇다면 x를 2로 바꿔치기 하는 것은 x 변수에 2를 저장하는 코드 뒤에서만 가능하다. 코드의 맨 밑에서부터 시작해서 여기까지 교체해 올라온다는 개념에서 전파라는 이름이 붙었다.

상수 전파에도 존 코크의 흐름 분석 기법이 사용된다.

죽은 코드 제거

프로그램을 작성하다 보면 의도치 않게 아무 의미 없는 코드가 존재할 때가 있다. 실제로는 수행될 가능성이 없거나 아무런 영향을 발휘하지 못하는 코드를 말한다.

int i = 1;
int j = -1;

int x = i + 10;

return x;

x = i + 20;

return x;

위의 코드를 보면 return x가 두 번 사용되었다. 당연히 첫 번째 return x 뒤에 오는 코드는 수행될 가능성이 없다. 죽은 코드이다. 그리고 변수 j는 선언되었지만 사용되고 있지 않다. 이것도 죽은 코드이다. 이런 죽은 코드를 컴파일할 필요는 없다.

존 코크의 흐름 분석 기법은 이런 죽은 코드를 찾아내는 데 사용되었다.

1 2 3 4 5 6 7