기타 업적
호프크로프트-카프 알고리듬
캘리포니아 대학교 버클리의 딕 카프와 함께 1973년에 발표한 이 알고리듬11도 역시 그래프와 관련된 알고리듬이다. 이 알고리듬은 이분 그래프bipartite graph에서 최대 크기의 매칭matching을 효율적으로 찾는 일을 한다. 세 개의 주요 단어를 이해해 보자.
이분 그래프
주어진 그래프에서 꼭짓점들을 두 개의 그룹으로 분리시켰을 때, 그래프에 있는 모든 변edge들이 두 개의 그룹에 모두 걸쳐지도록 만들 수 있는 경우가 생기면 이 그래프를 이분 그래프라고 부른다.

위의 그래프를 보면, 위쪽 꼭짓점 두 개와 아래쪽 꼭짓점 세 개가 하나의 그룹으로 묶여 있고 총 6개의 변edge들이 이 두 그룹에 모두 걸쳐 있는 것을 볼 수 있다. 따라서 이 그래프는 이분 그래프이다.
매칭
그래프 이론에서 매칭matching이란 그래프를 구성하는 변들 중에서 서로 접하지 않는(즉, 꼭짓점을 공유하지 않는) 변들을 뽑아내는 일을 말한다. 딱 한 가지 결과만 있지 않고 여러 가지 답이 나올 수 있는데, 보통의 경우는 변의 개수가 가장 많은 답, 즉 최대 매칭에 관심을 갖는다. 위의 그래프에서 매칭을 하면 아래와 같은 결과가 나올 수 있다.

위에서 초록색으로 나타낸 변들이 매칭에 해당한다.
효율
최대 매칭을 구하는 알고리듬으로는 포드-풀커슨 알고리듬이 사용되고 있었다. 이 알고리듬의 시간 복잡도는 ![]() 였는데 호프크로프트-카프의 알고리듬은
였는데 호프크로프트-카프의 알고리듬은 ![]() 이다.
이다.
스플레이 트리
조합적 최적화combinatorial optimization의 대표적인 문제 중 하나가 네트워크 흐름network flow 문제이다. 어떤 네트워크가 주어졌을 때 네트워크를 지나가는 데이터의 흐름을 최적화하는 방법을 찾아야 한다.
최적화의 기준은 여러 가지가 있다. 데이터의 양을 최대화한다거나 비용을 최소화한다거나 하는 식이다. 이 문제는 컴퓨터 네트워크만이 아니라 현실 세계에서도 쉽게 찾을 수 있다. 예를 들어 수돗물의 흐름을 최대로 할 수 있게 지하 상수도 관을 구성한다거나, 최대한 많은 차량이 다닐 수 있게 시내 도로망을 구성하는 일 등을 생각할 수 있겠다.
타잔은 그가 지도하던 대학원생인 대니얼 슬리터Daniel Sleator와 함께 네트워크 흐름 문제에 도전했다.5 이 과정에서 네트워크 흐름 문제는 복수 개의 이진 트리들을 탐색하는 문제로 변환되었다. 두 사람은 편향 이진트리biased binary tree라는 개념을 제안했다. 이것은 말 그대로 특정 노드에게 유리하게 자료구조를 구성하는 방식이다. 즉 노드(트리 그래프에서 꼭짓점을 의미한다)에 따라 탐색 시간이 달라지며 그 기준은 빈도frequency나 가중치weight를 따른다. 이 결과를 가지고 박사 학위를 받은 대니얼은 벨 연구소에 취직했다. 대니얼은 관련 연구를 계속 했고 자연스럽게 타잔도 합류했다. 결국 타잔은 스탠퍼드의 교수직을 내놓고 벨 연구소로 자리를 옮기기에 이른다.
타잔은 분할상환분석amortized analysis이라는 기법을 제안했다. 알고리듬의 복잡도를 따질 때 최악의 경우를 고려하는 것이 일반적이었는데 그러다보면 알고리듬을 구성하는 연산마다 최악의 경우를 가정하게 되므로 전체 알고리듬의 성능은 가장 최악인 상황에 의해 결정되곤 한다. 타잔이 생각하기에는 어떤 입력이 들어오느냐에 따라 어떨 때는 빠를 수 있기 때문에 알고리듬의 전체 성능이 특정 최악의 상황에 의해 결정되는 것이 바람직하지 않았다. 분할상환분석이란 알고리듬을 여러 다른 상황에서 수행하여 그 평균값으로 성능을 따지는 기법이다.
분할상환분석이라는 방법론을 배경으로, 타잔과 대니얼은 스플레이 트리Splay tree라는 자료 구조를 제안했다. 이것도 일종의 이진 탐색 트리인데 가장 최근에 접근한 정보는 더 빠르게 접근할 수 있도록 부가정보가 추가되었다. 이는 사실 휴리스틱한 접근방식이다. 가장 최근에 접근한 정보가 이른 시일 내에 다시 접근될 가능성이 높다는 것은 경험에서 얻은 지식일 뿐, 수학적으로 증명된 사실은 아니다. 하지만 효과는 매우 좋았다. 스플레이 트리에서는 노드 추가, 삭제, 찾기 작업의 시간 복잡도가 ‘분할상환 시간적으로’ ![]() 이다. 후에 두 사람은 스플레이 트리를 발명한 공로로 1999년에 ACM의 Paris Kanellakis 상을 받았다.
이다. 후에 두 사람은 스플레이 트리를 발명한 공로로 1999년에 ACM의 Paris Kanellakis 상을 받았다.
- *출처: https://cfcs.pku.edu.cn/english/news/240411.htm
- †출처: https://web.cs.toronto.edu/dls/2017-2018
- ‡출처: https://cfcs.pku.edu.cn/english/news/240411.htm
- §2020년에 튜링상을 수상했다.
- ¶1993년에 튜링상을 수상했다.
- #출처: https://pma.caltech.edu/documents/2620/1992_-_Robert_Tarjan.pdf
- **알골 W 언어는 당시 스탠퍼드 대학교 교수였던 니클라우스 비르트가 개발한 언어이다.
- ††2020년에 튜링상을 수상했다.
참고문헌
- 1.Hopcroft John E. Computer science: the emergence of a discipline. ACM Turing Award Lectures.:1986. doi:10.1145/1283920.1283943
- 2.Tarjan Robert E. Clinical and metabolic features and general principles of management. ACM Turing Award Lectures.:1986. doi:10.1145/1283920.1283944
- 3.A.M. Turing Award Oral History Interview with John E. Hopcroft by David Gries. ACM; 2018:24.
- 4.E. Hopcroft John, D. Ullman Jeffrey. Formal Languages and Their Relation to Automata. Addison-Wesley; 1969.
- 5.A.M. Turing Award Oral History Interview with Rober (Bob) Endre Tarjan by Roy Levin. ACM; 2017:49.
- 6.Hopcroft John, Tarjan Robert. Efficient Planarity Testing. J ACM. Published online October 1974:549-568. doi:10.1145/321850.321852
- 7.V. Aho Alfred, E. Hopcroft John, D. Ullman Jeffrey. The Design and Analysis of Computer Algorithms. Pearson; 1974.
- 8.Asymptotic definition and meaning. Colliins English Dictionary. Accessed March 16, 2023. https://www.collinsdictionary.com/dictionary/english/asymptotic
- 9.표준국어대사전. 국립국어원. Accessed March 16, 2023. https://stdict.korean.go.kr/search/searchView.do?pageSize=10&searchKeyword=%EC%A0%90%EA%B7%BC%ED%95%98%EB%8B%A4
- 10.Frenkel Karen A, Hopcroft John E, Tarjan Robert E. An interview with the 1986 A. M. Turing Award recipients—John E. Hopcroft and Robert E. Tarjan. Commun ACM. Published online March 1987:214-222. doi:10.1145/214748.214754
- 11.Hopcroft John E, Karp Richard M. An
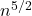 Algorithm for Maximum Matchings in Bipartite Graphs. SIAM J Comput. Published online December 1973:225-231. doi:10.1137/0202019
Algorithm for Maximum Matchings in Bipartite Graphs. SIAM J Comput. Published online December 1973:225-231. doi:10.1137/0202019
(c) 이재범, 2023
이 콘텐츠는 대한민국 저작권법의 보호를 받습니다. 작성된 모든 내용의 권리는 저자에게 있으며, 저자의 동의 없는 사용은 금합니다. 본 콘텐츠의 일부 혹은 전체 내용을 무단으로 전재/복제/배포하거나 2차적 저작물로 재편집하는 경우, 법적 책임을 지게 됩니다.



답글 남기기